金融网络中的系统性风险：一份综述

3.网络结构与系统性风险

　　我们现在讨论网络结构如何影响系统性风险。由于有关该问题的许多文献都是基于银行之间的债务网络，所以我们大多只关注基于银行间合约的相互依赖关系。

　　我们首先讨论股票价值下降和债务违约是如何连锁反应的，以及这种连锁反应如何取决于网络的结构和冲击的类型；然后，讨论源于自我实现类反馈（self-fulfilling feedbacks）的系统性风险，并详细阐述产生此类反馈的各种网络模式。

　　3.1网络密度的非单调性

　　金融网络中的反作用力使得传染在网络密度上具有非单调性。艾略特等人（Elliott et al.，2014）详细研究了这一点，它还适用于各种模型，包括西福恩特斯等人的模型 （Cifuentes et al.，2005；Gai and Kapadia，2010；Wagner，2010；Elliott et al.，2014；Gofman，2017；Jackson and Pernoud，2019）。网络密度的非单调性将金融市场中的传染与疾病或思想的传播区分开来，对后者来说，增加互动只会导致更广泛的传播。（*20.这也超出了所谓复杂传染的范畴，复杂传染是指需要多次相互作用才能导致传染的事件，例如，听到几次谣言才能信谣并传谣，或者跟随大多数朋友的行动\[相关背景讨论和参考资料见Centola（2018）和Jackson（2019），关于复杂传染如何随网络而不同的详细讨论，参见Jackson and Storms，2017\]。 金融网络具有复杂传染的因素，因为银行可能只有在数轮交易对手违约后才会破产，而且相互作用的次数也具有非单调性。）

　　随着交易对手的增加，银行变得容易受到价值下降或更多违约来源的影响，这往往会加大发生连锁反应的可能性。然而，在一家银行的总风险敞口不变的情况下，将风险敞口分摊到更多的交易对手身上，可以降低银行对特定交易对手的风险敞口，从而降低危机蔓延的可能性。为了研究这两种力量，艾略特等人（2014）区分了金融机构之间互联互通的两个基本维度：（1）每个机构有多少个合作伙伴，他们称之为网络密度；（2）银行投资组合中与其他机构签订合约的部分，他们称之为网络整合。

　　我们用一个简单的例子来说明这两种力量的非单调性。考虑一个由相似银行组成的网络，它们的资产负债表如图3a所示。

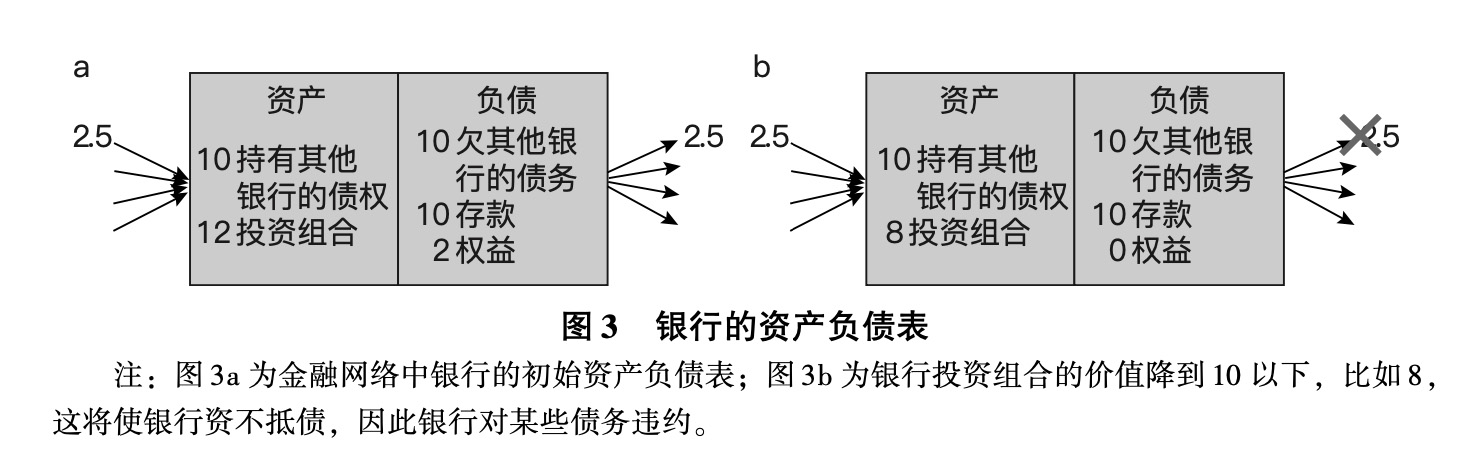　　在负债方面，每家银行有10单位的存款，欠其他银行10单位的债务，银行所有者有2单位的权益。在资产方面，每家银行都有价值12的投资组合和价值10的其他银行的债权。

　　在这个例子中，我们可以将网络整合度测量为10，即银行的资产中有多少来自其他银行，在该例子中是以银行间债务的形式。这家银行的网络密度为4，即银行的交易对手的数量。因此，这些网络整合度和网络密度导致每个交易对手的风险敞口为2.5单位。在这个例子中，银行还欠四个交易对手每人2.5单位，因此是完全对称的。

　　现在我们假设其中一家银行的投资组合价值下降，如图3b所示。这家银行现在资不抵债，所以它无法偿付所有债务。就本例而言，由于破产成本，我们将至少一笔贷款的违约视为总违约，尽管显然可以将该示例扩展到处理部分违约。

　　最初，这家银行欠四家不同的银行各2.5单位，因此它至少有一笔贷款没有偿付。这笔违约贷款必须由向第一家银行提供贷款的对手方冲销，因此第二家银行损失了2.5单位的资产。第二家银行现在也已经资不抵债，并且拖欠了一些付款。再一次，让我们假设存在破产成本，银行无法偿还至少一笔贷款，如图4a所示。这就是违约的连锁反应。

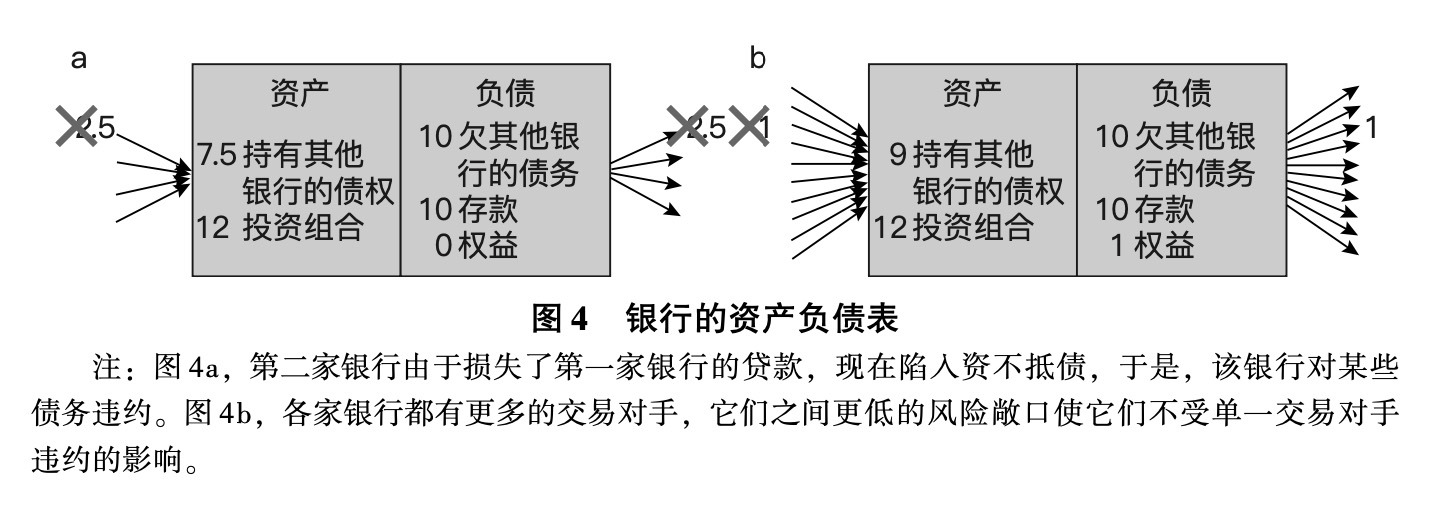　　由于银行相互之间的风险敞口为2.5，初始权益价值仅为2，各家银行甚至容易受到单一交易对手违约的影响。在本例中，网络整合度和网络密度都是驱动违约的重要因素。如果银行的网络整合度较低，但密度相同，那么它们对任何给定交易对手的风险敞口都将小于2.5。如果小于2，那么任何单一交易对手违约都不会耗尽一家银行的权益。整合度的提高，也就是说，每家银行对其他银行的风险敞口的增加，往往会加剧传染，就像在这个例子中一样。（*21.然而，正如Elliott et al.（2014）讨论的，通过改变银行经由其相互连接关系而隐性持有的资产，提高整合度有助于使给定银行的投资组合多样化，这取决于具体情况。因此，更多的风险敞口有助于使给定银行的投资组合多样化，使其投资更少波动、更稳定，但也导致传染的可能性增大。）

　　类似地，如果银行的网络整合度仍然是10，但密度更大（即更多的合作伙伴），因此，它对任何单一交易对手的风险敞口不超过2，那么连锁反应也将被避免。为了了解密度的重要性，让我们改变例子，使每个银行有10个交易对手，并欠每个对手1单位债务，如图4b所示。因此，整合度相同，但密度增加了。在这种情况下，不再有任何连锁反应。任何单一交易对手的违约不再导致银行破产。

　　这里我们可以相当清楚地看到非单调性。我们增加了每家银行的交易对手数量，使金融网络更加密集，但我们消除了连锁反应。传染是非单调的，因为如果一开始没有交易对手，就不会有传染。或者，如果我们只有两家银行，彼此配对，那么一家会拖累另一家，但影响不会扩散。有四个交易对手的情况达到了一个平衡点（sweet spot）：交易密度高到足以形成一个非常紧密的网络，在这个网络中，事情可以广泛传播，每家银行的风险敞口足以使一笔违约就可能导致交易对手破产。一旦我们增加到10个交易对手，那么一笔违约对任何一个交易对手都不再是大问题。

　　投资组合中的相关性消除了多样化带来的好处，提高了共同的脆弱性，从而减轻甚至消除了传染中的这种非单调性。为了说明相关性的作用，重新考虑上面的例子（见图4）。假设银行的投资组合表现出显著的相关性，这也许是因为它们都有大量相同的债务抵押债券的敞口，就像2007年的情况一样。例如，假设一家银行的投资组合低于10，其他银行的投资组合也可能低于正常水平。如果我们将图4b中所示的第二家银行的投资组合降到10，同时将第一家银行的投资组合降到8，那么第一家银行的违约就足以将第二家银行推入破产境地，如图5所示。此外，银行资产负债表中的资产进一步降低，这不仅是因为它们的投资组合表现不佳，还因为它们所欠的债务不止一笔同时违约，而这又是因为各银行的价值是相互关联的。（*22.关于其他相关投资组合对系统性风险产生影响的例子和模拟，可参见Elliott et al.（2014）的在线附录。）

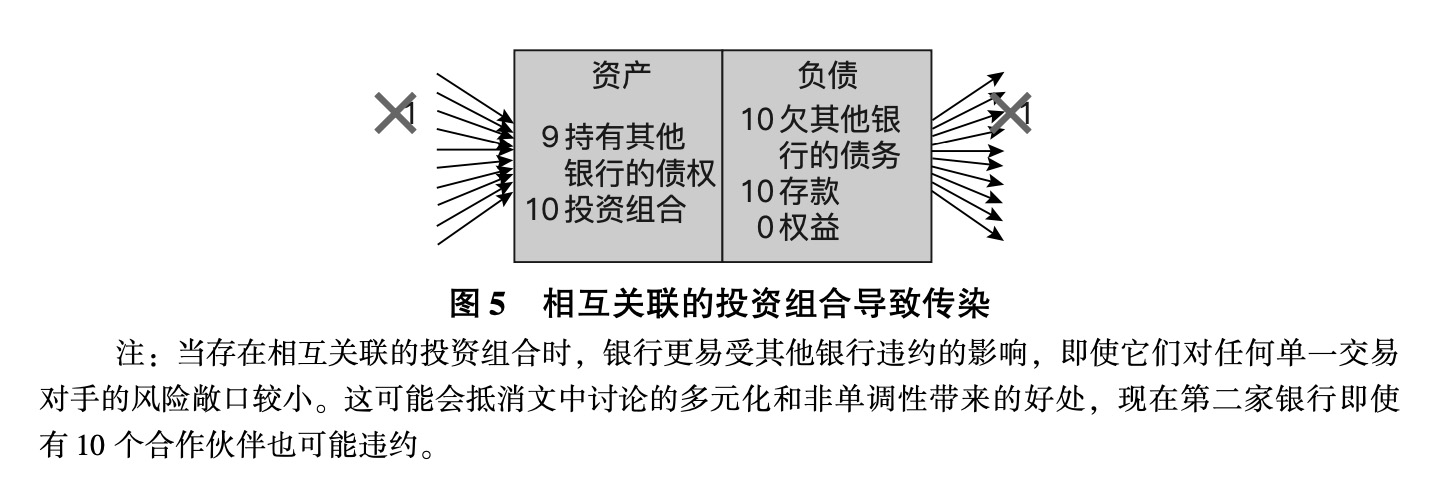　　理解这种效应的一种方式是，银行间投资的正相关性会抵消交易对手多元化带来的一些好处，并促进传染。更一般地说，增加投资组合的相关性会提高出问题的概率。例如，瓦格纳（Wagner，2010）考虑了两家银行和两种资产，并观察到如果两家银行通过平均配置两种资产来分散其投资组合，那么它们的投资组合是完全相关的。因此，这里存在一个权衡，因为更多元化伴随着银行投资组合之间更强的相关性，会降低每家银行的无条件违约概率，但会提高它们一起违约的概率（假设它们一开始就投资于不同的资产），从而加大系统性风险。当然，最糟糕的情况是银行的投资组合类似，不够多样化，例如，它们都持有类似的抵押贷款或贷款，因为这些投资组合是相互关联的，且风险很大。

　　3.2稳健但脆弱

　　正如霍尔丹等人（Haldane，2009；Gai and Kapadia，2010）详细研究的那样，金融网络具有“稳健但脆弱”的属性。（*23.Callaway et al.（2000）较早研究了渗流对图（percolation on graphs）以及这种权衡。）例如，银行之间以贷款或提供流动性的形式相互依赖，从而允许风险分担，这可以帮助单个机构更少受到单个流动性或投资组合冲击的影响。这些冲击在交易对手之间传播，交易对手的多元化有助于降低单个机构的失败概率。从这个意义上说，金融网络是稳健的。然而，非常大的冲击可能导致某个机构破产，尽管交易对手多元化，但相互依赖可能使冲击的传播更普遍、更广泛。当然，这其中有细微差别，取决于模型和机构之间的合同类型（Allen and Gale，2000；Gale and Kariv，2007；Gai and Kapadia，2010；Battistoni et al.，2012；Elliott et al.， 2014；Acemoglu et al.， 2015a）。

　　这与上面讨论的非单调性有关，但又有所不同。稳健但脆弱的特性意味着，在某些情况下，一个网络可能促进了另一个网络，而在另一些情况下，它却可能使情况变得更糟。在上述关于非单调性的讨论中，我们考虑了网络中的变化如何影响某一特定冲击是否产生连锁反应，因此，这是假定冲击不变时对网络的比较静态分析。相反，稳健但脆弱的现象则是要比较某一个特定网络如何应对不同类型的冲击。

　　阿西莫格鲁等人（Acemoglu et al.，2015a）关注银行间无担保债务网络，并研究银行收益遭受的冲击如何通过网络传播。他们区分了两种冲击：小到足以被金融体系中的总过剩流动性吸收的冲击和不能被吸收的冲击。在前一种类型中，相互依赖明显减轻了危机蔓延的风险：最能抵御危机蔓延的网络结构是全连接网络（complete network），在这个网络中，每家银行的总负债平均分布在所有其他银行。这将导致最大的风险分担和最小的预期违约数量。然而，如果冲击大于金融体系中的总过剩流动性，相互依赖只会促进冲击的传播。我们可以在艾伦和盖尔（2000）的分析中看到这一点。该分析表明，在一个更具体的环境中，冲击蔓延的风险取决于流动性需求是否存在总体不确定性。如果总体不确定性并不存在，那么银行间的联系将使银行可以分担更多风险而不会产生系统性风险。

　　卡夫拉莱斯等人（Cabrales et al.，2017）强调了冲击规模的作用，在他们的模型中，银行之间的相互依赖就是其投资的相关性。他们考虑的是一组事前相似的银行，每家银行都有外部债务，并能接触到有风险的项目。这些项目的回报受到的冲击在各个银行间是独立同分布的。如果一家银行无法偿还外部债务，它就会违约，并因陷入困境而产生一些成本。银行可以通过交换对彼此项目的债权来实现投资组合的多样化：从i到j的连接表示i银行对j项目的收益索取权。因此，在卡夫拉莱斯等人的模型中，银行和项目之间的连接表示银行间投资组合的相关性，而不是银行间债务。于是，同样的权衡就出现了：更多的连接可以更好地分担风险，但也意味着暴露在更多的风险中。何种网络结构的预期违约次数最少，由冲击的分布决定。特别是，卡夫拉莱斯等人（2017）表明，如果存在较大的冲击，则空网络（empty network）是最优的。如果冲击大多较小，那么完全对称网络是最有韧性的。其他的冲击分布可以产生使传染最小化的中等网络密度。

　　阿西莫格鲁等人（2015a）描述了在不同冲击类型下对传染最有韧性或最没有韧性的网络结构。如果冲击很小，整个网络的传染风险最低。相比之下，环形网络是最容易传染的网络结构，在环形网络中，每家银行的债权都集中在一个交易对手身上。该分析适用于常规网络，即所有银行的银行间债权与负债数量相同，交易对手数量相同。这排除了银行规模和关联度的异质性，以及银行成为净贷款人或净借款人的可能性。

　　为便于分析，一种处理方法是限于对简单情形的归纳总结。另一种方法是利用大型随机网络的特性。这两种方法都可以提供有价值的见解且具有可操作性，但只适用于有限类别的网络。

　　一个挑战是，金融网络经常涉及重大的不对称性，比如存在核心-外围结构，这影响了传染的风险。大型核心银行可以抵御小冲击，但当遭遇大冲击时，尤其是当这些冲击相互关联时，它们可能会遭遇灭顶之灾。这一点很重要，如艾略特等人（2014）通过模拟研究，证明了核心-外围网络也可以消除第3.1节中讨论的非单调性的某些方面，其原因在于，如果核心银行对某一个大型银行或实体有大量风险敞口，那么这家银行或实体的倒闭可能导致核心银行内部的广泛传染，然后蔓延到整个系统。这就是2008年出现的情况。也有其他研究提供了证据，证明异质性至关重要。例如，有模拟研究（Gai et al.，2011）表明，传染随银行间债权网络的集中度而变化。还有研究（Glasserman and Young，2015）提供了一些理论结果，表明在某一类网络中，当银行的规模不同且冲击源自大型银行时，传染是最大的。另有研究（Teteryatnikova，2014）说明了相邻银行连接度（即交易对手的数量）之间的负相关有助于提高网络的韧性。

　　鉴于分析的复杂性，我们有必要从两个方向继续我们的分析：一个方向是深入了解网络结构的异质性如何影响金融传染，以及通过具体的应用，为了解普遍存在的重要网络特征提供经验研究方面的背景。另一个方向是将传染模型应用于观察到的网络，以模拟风险模式，监管机构越来越倚重这种方法（Aikman et al.，2009； Basel Committee on Banking Supervsion，2015）。

　　3.3自我实现的反馈效应和信贷冻结：循环的作用

　　接下来，我们将讨论网络结构如何影响第二类系统性风险：导致多重均衡的自我实现的反馈效应。

　　目前正在兴起的一类文献强调了循环在生成多重均衡中的作用（Roukny et al.，2018；D’Errico and Roukny，2019；Jackson and Pernoud，2020），如图2所示。在银行间债务网络中，循环会增加交易对手风险，却不会在金融体系中创造价值；因此，清算循环在不影响银行价值的情况下降低了连锁违约的风险。例如，有研究（Roukny et al.，2018）表明，当且仅当存在一个由充分互联的银行组成的循环，即一家银行的偿付能力依赖于循环中前一家银行的偿付能力时，银行价值才存在多重均衡。

　　作为一个例子，请考虑图6所示的金融网络。在图6a的金融网络中，如果没有银行偿付其债务，那么假定每家银行的投资组合价值为10，小于银行所欠的债务，则没有一家银行能清偿债务。所有银行都资不抵债，没有债务得到清偿就成为一个自我实现的均衡。另一个均衡是所有债务都得到偿还。相比之下，在图6b的金融网络中，总债务被勾销，只剩下净债务。此外，还有一个独特的均衡，在这个均衡中，所有银行都有偿付能力。清除所有的循环消除了多重均衡的可能性，并确保只有最好的均衡。因此，清算循环可以带来巨大收益，特别是当人们预期银行和更广泛的投资者持有悲观信念或者相信他人持有悲观信念时。

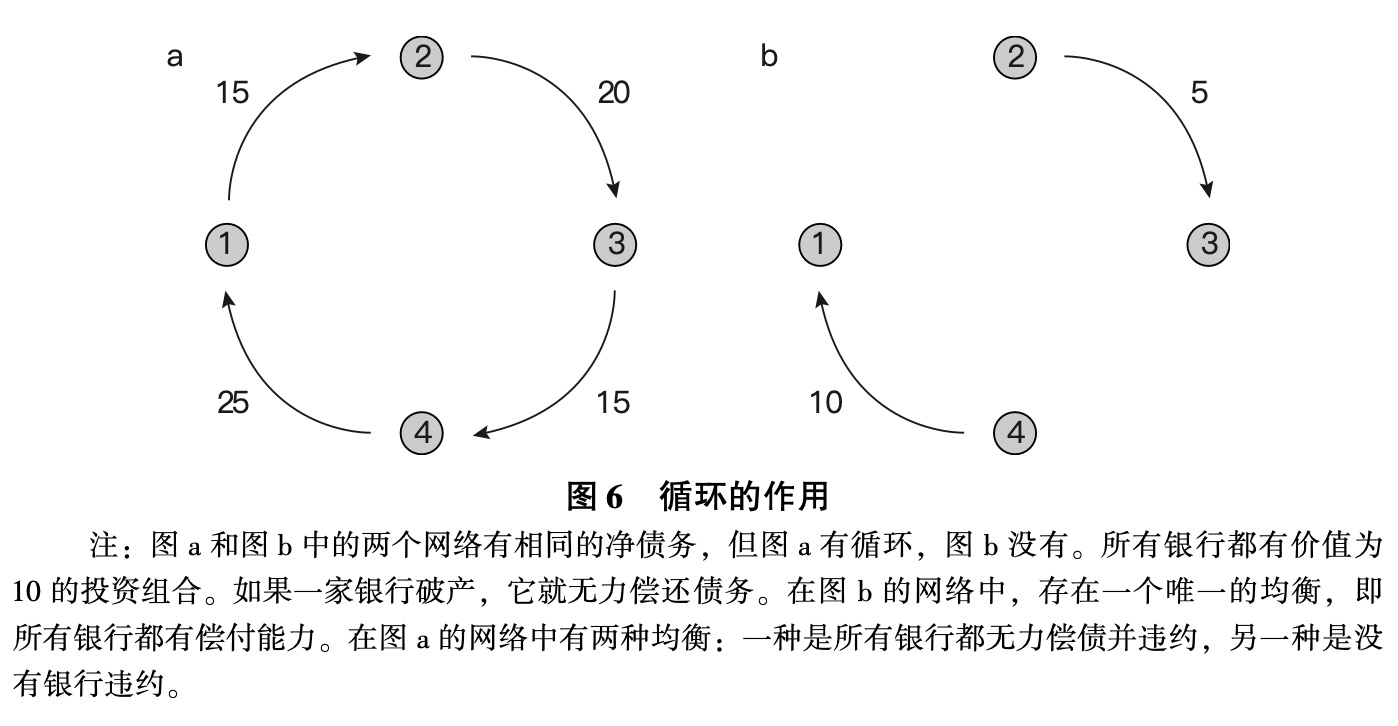　　当然，这是一个典型例子，以表明银行如何消除其债务，并避免坏的均衡。然而，在实践中，这些循环要复杂得多，涉及许多银行、不同的债务期限或合约类型，以及可能导致惯性和协调失灵的其他因素，特别是在时间不确定和人们延迟偿还债务的情况下。因此，重要的是要了解什么时候循环会出现问题，以及当循环存在时如何克服它们。

　　杰克逊和佩尔努（2020）详细研究了自我实现的连锁效应和信贷冻结，并描述了它们如何依赖于循环的存在、银行的投资组合，以及与破产相关的成本和延迟。（*24.在不存在破产成本的情况下，银行价值通常是唯一的（unique，Eisenberg and Noe，2001）。）如果一些银行的总风险敞口较小，这种自我实现的连锁反应和信贷冻结就不太可能发生，因为这些银行可能有足够的资本作为缓冲，阻止连锁反应。如果某个循环中没有一家银行有足够的外部资产来触发该周期内的连锁偿还，就会出现自我实现的反馈效应。杰克逊和佩尔努 （2020）也考虑了银行之间更一般的金融合约，并描述了多重均衡的存在，表明它们是由一种特定类型的循环产生的，其中涉及一些债务，但也可能涉及其他合约。但是，他们表明，不涉及某些关键债务义务的周期性结构不可能导致多重平衡。这种对网络周期性结构的描述不仅解释了多重均衡和信贷冻结，而且为确定使金融网络恢复偿付能力所需的最低救助提供了基础，如下文所述。

　　清算循环带来的收益可以解释投资组合压缩（portfolio compression）这种风险管理技术的使用（D’Errico and Roukny，2019）。该技术包括旨在减小银行间总风险敞口以降低监管要求的净额结算机制。类似的观点也经常用于讨论通过中央结算对手方（CCPs）结算双边场外交易（OTC）的好处。集中交易平台允许银行间合约的多边净额结算，这提高了金融网络的透明度，并限制了交易对手风险。（*25.更详细的讨论和背景资料可参见Duffie and Zhu（2011），关于中央对手方保证金和抵押要求的更近期研究，可参见Capponi and Cheng（2018）和Wang et al.（2020）。）如果银行间合约仅限于债务合约，这种多边净额结算属于结算循环，如图6所示。