传染控制的经济学

3.模型的构建与运用

　　3.1外部性：对传染加以公共控制的主要动机

　　当人们出于自利做出个人决策时，他们只会考虑直接影响自己的因素。他们对预防和治疗的选择会考虑自身（或许还有较为亲近的人）的收益与成本，但不包含其他人的收益与成本。由于每个人都只是群体中的一员，各人的决策对传染病的总体变量仅有极微小的影响，所以各人不会考虑自身决策导致的传染病变化再产生的影响。可是个人的决策加总起来，却会导致传染病的流行，人们的决策加总起来会对其他人的福利产生作用，形成感染的外部性。因此，个人的决策未必是社会最优结果。经济学家沿着外部性思路采用的理论概念，也就不同于流行病学家采用的羊群效应、质量效应或社群效应等说法。

　　对于私人激励与社会激励的差异，福利经济学的解决方案是对具有利他福利效应的个人行为提供补贴，而对损害他人利益的个人行为征税。由此继续让个人做决策，但其激励会有所调整。本来不在自己考虑范围之内的社会后果，通过补贴或税收的干预，将内化为个人自己关注的内容。

　　从机制上讲，测算这种补贴或税收体系的一种办法是三阶段操作：第一阶段，假设社会计划者可以实际控制健康方面的所有决策，通过目标函数（通过对众多个人福利水平的某种测算）的最大化测算出社会最优水平。最重要的一点是，社会计划者会考虑决策对传染病总体发展的影响，这种测算通常由不同学科的应用控制理论家（包括流行病学家）完成，针对不同感染场景，并有悠久历史（Wickwire，1977；Sethi and Staats，1978；Wiemer，1987）。第二阶段，测算出个人在最大化其目标函数时的行为选择，但不考虑对传染病的总体影响。第三阶段，测算出要让个人决策等同于社会计划者的选择，使社会计划者测算出的理想结果能分解到个人决策者，应该在第二阶段安排多少补贴或税收。后两个阶段的操作是福利经济学方法的真正标志，较少得到应用，并且很自然地只是由经济学家采用。（③有学者设计的模型让面临感染风险的决策者做最大化选择（Chen，2004；2006a，b；2009；Chen and Cottrell，2009），以此考察参数变化对感染率的影响，但不涉及对决策者福利的影响，也未讨论如何能对个人激励加以调整，使其采取社会最优水平的决策。） 本节其余部分将介绍开展此类三阶段分析的现有成果。

　　当然，以上关于约束条件的讨论（第2.1节到第2.4节）中提到，对于传染病采取此类补贴或税收干预未必可行，至少有时不能直接针对社会和私人的成本收益差异。假如没有看到这一事实，没有对模型做相应扩展，则可能导致外部性概念变成一个很模糊的比喻，而不能给实际干预措施的设计提供真正借鉴。例如在性传播疾病中，我们不能对有风险的性行为本身征税，而这在理论上是社会计划者解决方案实施的目标所在。并且与依靠信息采集技术的进步、通过收费来控制交通拥堵和污染的伦敦交通区划方案不同，上述事实显然难以通过监督技术的改进予以克服。对许多健康相关的行为而言，征税或补贴的困难源于其内在本质，技术革新不足以解决问题。我们可以对购买避孕套提供补贴，但这一补贴不等同于给在危险性行为中使用避孕套提供补贴，人们不可能也不愿意直接监督后者。无论如何，免费发放避孕套或许仍不足以使其达到最优使用水平，甚至花钱请人们取走避孕套也不等同于就能使其得到利用。当社会计划者的最优解决方案出于此类原因无法实施时，表面上合意的选择反而会使情况变得更糟，给我们提出次优选择问题。

　　外部性理论在疫苗上的应用，给许多类似问题提供了一个很好的案例。如果能找到疫苗，它将是一种关键的生物医学干预手段。疫苗的建模相对简单，至少对一阶近似是如此，因为这是一个二选一的决策。对疫苗政策的分析可以具体揭示如何把传染病控制模型的各个部分组合起来。对人们是否遵从干预措施可以做较好的监督，因为疫苗接种是由专业医疗人员完成的。另外尽管必须配合接种，但如果获得免疫力只需要一次注射，则不需要更多的服从配合。对疫苗接种的研究充分揭示了外部性对激励政策的影响。但事实上，某些学者认为在疫苗问题上，并不存在外部性导致的公共政策合理性。对这一观点的考察非常有益于我们了解感染的外部性的本质。

　　3.2疫苗接种模型

　　给人们提供传染病疫苗接种的公共计划经常被作为用政策克服外部性的绝好案例，这是因为人们通常不会考虑自身获得免疫力后，不再会感染他人带来的收益。然而菲利普森（2000，第 1763—1764页）不同意这一基于外部性的说法：

　　的确，根据对疾病预防的正外部性的正统观点，经济学家通常支持对传染病预防采取积极的公共行动……然而，他们很少尝试去解释疾病发生模式，或者在个人根据约束条件做出最优决策的社会中对公共干预效果加以评估。近期开展的此类研究则质疑了经济学古老教科书中的观点……

　　弗朗西斯（Francis，1997）在考察疫苗接种时，首次对传染病控制做了规范的动态分析，把社会最优与私人最优做对比，以考察外部性的本质。他强调，如果有任何组别给易感染者造成外部性，那是来自被感染者，而非未接种的易感染者。因此他指出，需要把从易感染者到被感染者的转化明确纳入动态模型，才便于理解外部性，这也表明芬恩和克拉克森等人（Fine and Clarkson，1986；Brito et al.，1991；Xu，1999；Kureishi，2009）的研究采用静态分析方法有其不足之处。

　　不过在弗朗西斯（1997）的模型中，并不存在外部性，或者说不存在证明需要政府干预的外部性。实际上，他的假设似乎是有意识地为激发未来的研究而设计的。他假设，不存在无感染和无免疫力的新生人口，因此易感染人群没有这一输入量；另外没有人从感染中康复，也没有人因为任何原因死亡。这套关于健康状态转化顺序的假设成为其结论的核心。在弗朗西斯的模型中，成本和收益都是贴现值，如果感染率较低，疫苗接种的即期收益也就较低，所以把疫苗接种的成本推迟就是值得的。

　　我（2003）之前对弗朗西斯的上述结论做过如下直觉描述：如果没有新生和死亡，也无人接种疫苗，则感染会扩大——如公式（1）的描述——因此易感染者所占比例会持续下降，被感染者所占比例持续上升。随着被感染者比例的上升，剩余易感染者被感染的风险将增加，通过疫苗接种获得免疫力的收益也会提高。最终，被感染者所占比例（感染率）会达到一个临界值，使接种疫苗的收益等于接种疫苗的成本（后者为常数）。无论是从社会还是个人视角看，如果任何人接种疫苗是值得的，那么对所有易感染者接种疫苗也都是值得的，因为如果不这样做，被感染者所占比例（以及易感染者被感染的概率）仍会继续提高。总体感染率不可能下降，因为没有新出生的易感染者，没有被感染者的康复或死亡，这些都是关键的状态转化假设。此时，让感染率维持稳态水平的唯一办法，就是一旦达到临界值后对所有易感染者接种疫苗。因此在稳态情形下，易感染者所占比例为零。

　　由于临界值对社会行动与个人行动而言是相同的，就不存在外部性，至少不存在表明需要干预措施的外部性。或许有人会推测，政府可能希望把临界值设定在更低水平，以更早达到。但为什么要这样做呢？政府为了使感染率达到临界值，需要给所有人接种疫苗，因此没有易感染者会因为感染率的不再提升而受益。换言之，一旦达到私人临界值，每个人反正都会接种疫苗，而如果每个人都会接种，也就不会有人因为降低总感染率而提前接种并由此获益。所以政府提前给所有人接种疫苗并无意义，政府和私人的临界值是相同的。

　　我之前的研究分析了如下情形，有新出生人口，有死亡人口，但死亡人数仅为现存人口的一定比例，任何组别的人都呈渐进式死亡，这是数理流行病学中为数学处理而采取的很传统的假设（Gersovitz，2003）。上述关于出生和死亡的假设是与弗朗西斯模型（1997）的唯一不同之处，关键在于，依旧假设被感染者从来不会康复。

　　假如政府像社会计划者那样采取行动，可以控制谁接种疫苗，它将最大化汉密尔顿函数的现值（Gersovitz，2003）：

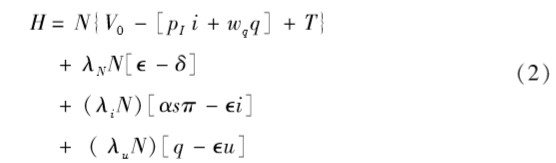　　公式（2）的第一行是社会计划者的目标：V0是某人在无感染情况下的效用的货币价值，pI是受到感染造成的成本（因此这一目标比有非健康产品支出的状态依存效用函数更简单），i是所有N个人中被感染者所占比例，wq是包含所有税收或补贴在内的疫苗接种的成本（对社会计划者而言，等于实际发生的成本pq），q是所有N个人中目前被接种者所占比例，T是因为wq与pq的差异而发生的税收或补贴总和（对社会计划者而言，为0）。公式的第二行是附加拉格朗日乘数λNN，表示总人数N的变化，其中为出生率，δ为死亡率。第三行是附加拉格朗日乘数λiN，表示感染者所占比例i的变化，其中对社会计划者而言，π = i；s是易感染者所占比例；α与公式（1）中的含义相同。第四行是附加拉格朗日乘数λuN，表示曾经接种疫苗且目前仍存活者所占比例u的变化。请注意：i+s+u=1。

　　公式（2）的汉密尔顿函数可以推导出社会计划者实施疫苗接种最优策略所需的标准条件。最优解确立了一个由疫苗接种维持的稳态感染水平，不是所有易感染者都会获得接种。如果认为稳态情况下的最优选择是对每个人都接种，则会导致矛盾。因为若采用普遍接种策略，对所有新出现的易感染者接种，则会稀释被感染者在总人口中所占比例，把感染率降低到稳态水平之下，而这一结论与在稳态感染率水平上每个人都接种疫苗的概念相悖。因此社会计划者的最优策略是对

　　一定比例的易感染者接种疫苗，该比例严格小于1，一旦达到稳态感染率，则继续对包括新生人口在内的易感染者实施部分接种，并使易感染者、已接种者和被感染者所占比例保持不变。

　　对于典型的个人，可以理解为同社会计划者一样用公式（2）的汉密尔顿函数来决定何时接种疫苗，只是个人把π视为外生因素（尽管由于其具有典型性，π应该等于i）。另外，如果政府对接种疫苗提供补贴，以比率tq＜0把最优决策做分散化处理，则有(wq-pq) = tqpq，而且T不等于0。典型的个人最优决策还涉及稳态感染率，但如果没有干预，则不同于政府的目标。没有政府干预时，私人临界值会高于社会临界值，因为前者未包含对其他人受感染的总体概率的影响。当政府对最优稳态做分散化决策处理时，会对疫苗接种提供补贴，并做如下设定：

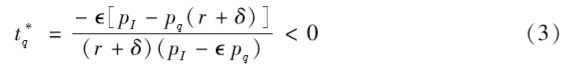　　事实上，出生人口给总人口带来了异质性：不是所有人都生活在同一时刻，未出生的人也不能与已出生的人一起做决策。只要出生率为正，无论其是否超过死亡率，无论总人口增长是否为正，都会得到补贴为正的结果。

　　我之前的研究还表明，如果被感染者康复后再度成为易感染者，康复可能起到与正出生率类似的作用，导致外部性，给政府干预提供理由，得出与公式（3）类似的推导结果（Gersovitz，2003）。与人口出生和死亡的问题相似，同弗朗西斯模型（1997）的主要区别在于是否存在向易感染人群转化的假设。在两种情形下，补贴的绝对值都负向取决于疫苗接种的成本和利率，正向取决于感染的成本，但与转化参数α完全无关。补贴的绝对值正向取决于出生率，在前一情形中负向取决于自然死亡率，在后一情形中正向取决于康复率。

　　在这两个模型中，政府干预的目标都是通过降低疾病流行水平，提高福利。只有当感染的成本无限大，或疫苗接种的成本为零时，政府的最优稳态感染率才会等于零，使传染病被完全消灭。但这只能是渐进的形式，因为被感染者人群只会逐渐消失，每个时期只有固定比例的被感染者死亡或康复，这是为数学处理而设定的假设的结果。还有，在感染成本无限大或疫苗接种成本为零的情形下，政府稳态与私人稳态重合，而且由于稳态感染率都是零，彻底消灭传染病并不需要政府的干预。

　　弗朗西斯与布里埃等人（Francis，2004；Boulier et al.，2006）的研究提供了更多关于外部性与疫苗接种的例子。在他们的模型中，人们的健康状态可以从易感染者转化为：（a）若接种疫苗，成为已接种并免疫的状态（布里埃等人的研究中允许出现疫苗接种失败）；（b）被感染后康复的状态。没有贴现，因此接种疫苗的任何人都是在传染初期被接种，但弗朗西斯设置了一个（有能力约束的）疫苗接种最大比例；也不存在人口出生和死亡。这些假设是特定的，但对于相比利率、出生和死亡来说进程较快的传染病，或许是较恰当的近似描述。这两篇论文的主要关注点都是季节性流感，而且作为求解技巧做了一个附加假设，即传染病在最优化期限内（当t=∞）会接近稳态。不过即使对季节性流感等疾病而言，该假设仍存在争议，因为我们不能假定流感季节结束正好是对应模型的稳态趋近，而非随着天气或人们行为的变化导致感染出现季节性减少。

　　还有研究提出了另一套假设条件（KribsZaleta and VelascoHernandez，2000），模型采用固定的疫苗接种率，但如果疫苗只是部分有效，会导致多重稳态结果。该模型中存在人口出生和死亡（但不是由感染本身导致），出生始终等于死亡，所以不存在人口净增长。人们会从感染中康复，再次成为易感染者，疫苗只能提供部分免疫力，免疫力随时间递减。疫苗接种率不是最优决定的，因此接下来的问题是：如果对多大比例的人进行疫苗接种做出最优选择，稳态是否有唯一解。后来的研究（Chen，2006a；Chen and Cottrell，2009）考察了与上述相似的模型，但假设人们在感染后不会康复，个人做最优化决策，仍会在这些条件下出现多重稳态的结果。不过后来这些研究未考察社会计划者的问题，也就没有发现外部性。布里埃等人（2006）的研究同后面两篇论文在多重稳态方面的结论差异或许在于，布里埃等人的最优化是在期初完成，而且由于人口不存在流入和流出，疫苗接种不需要持续开展。

　　我们做个对比：以上研究的结论是通过补贴把传染病控制在一定水平，但不是彻底消灭；而吉奥法德等人（Geoffard and Philipson，1997, 第 222页）则认为，由于无法根除传染病，“通过庇古税类型的补贴解决因为正外部性而供给不足的疫苗接种问题，这一经典理由应值得商榷”。（④在Geoffard and Philipson（1997）的模型里，人口的一定比例会死亡，这使任何组别都不会在有限时间内全部死亡，因此该模型中的疾病消灭最多是渐进式的。此外，他们在疫苗需求的异质性假设之下没有提供关于消灭传染病的社会最优结果，故难以将其结论同我的研究（Gersovitz，2003）做直接比较。最后，在假设疾病可以在有限时间内消除的关于根除疾病的简短讨论中，他们没有分析消灭疾病在何时是最优解，而只是对其成本和收益的上限和下限做了较弱的分析（Geoffard and Philipson ，第227页）。 ）其实，根除传染病的政策并不意味着通过补贴最优化地抵消外部性的政策。相对于收益而言，根除疾病的代价可能过高，但仍有充分理由通过最优化的疫苗接种补贴来减轻传染病的流行程度。而且根据那些假设感染只会渐进式消失的现有模型，当根除疾病在有限时间内可行时，首要研究任务之一仍是对疫苗接种做建模分析。（⑤Barrett and Hoel（2007）讨论了在有限时间内消灭传染病的情形，但其模型设定存在疑问。如果被感染者是终生携带者，则在目前的所有被感染者都死亡之前，疾病不可能完全消灭，而描述疾病消灭可能需要叠代模型。假如人们可能康复，则疾病消灭至少要求足够的时间，使最后一名被感染者康复或者死亡。这些是细微的必要条件，在有限时间内消灭疾病的模型必须将它们纳入考虑。然而Barrett and Hoel的模型设定并未明确，受感染的每一个人将如何在有限时间内死亡或康复，以及如何能实现疾病消灭。他们在其文献的第631页引入了公式（3），似乎是作为在有限时间内死亡或康复模型的替代机制，并将疫苗接种作为唯一的干预手段。但根据我对此问题的理解，这种模型设定缺乏从一种健康状态到另一种健康状态（易感染者、被感染者、康复者、免疫者、被接种者、死亡者等）的流行病学转化机制基础，以实现有限时间内的疾病消灭。尤其是，该公式似乎意味着疫苗接种会直接让人们脱离被感染者（而非易感染者）群体，因此也有与Francis（1997）的研究类似的谬误。）

　　在这一阶段，弗朗西斯与菲利普森（Francis，1997；Philipson，2000）的研究对疫苗接种外部性理由的反对，除一个不能广泛适用的案例外，似乎不具有普遍性。他们的观点更多是出于学术探讨，是对未来研究的启发，而非政策指导。当然，要描绘与疫苗接种有关的外部性影响的全貌，还需更多努力。

　　3.3更普遍的预防与治疗模型

　　在人们可以阻止传染的预防行动中，疫苗接种只是一个选项。另外，被感染者还可以接受治疗。对于通过随机同质性匹配实现人传人、被感染后不能康复或康复后可能再度被感染的反复传染（SIS）疾病，被感染者的比例将由如下公式决定：

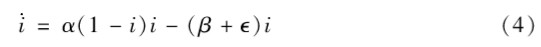　　对这一数理流行病学重要公式的推导，可参见我和哈默（Gersovitz and Hammer，2004）的研究。上式右侧的第一项对应公式（1）中用比例π=i表示的新感染者；第二项表示康复后重新成为易感染者的比率β，和新出生后成为易感染者的比率ε。

　　预防和治疗选项的自然表述是让α与某种预防投入a挂钩，该投入的增加会降低α的数值，另外使β与某种治疗投入b挂钩，该投入的增加会提高β的数值。与大多数研究文献不同，这一设定不是要么做要么不做的选择，而是让投入成为一个连续变量，这种性质能对应医疗支出的广泛区间变化，并具有边际收益递减的特征。除贴近现实外，该假设还为最优化问题提供了凹性函数基础，尽管仍不能保证问题可以求解。这种设定不同于从患者内省（意即让人们自己出去找到一个处方，为其付款，并遵照执行）中产生的僵化假设，更能代表为实现类型广泛的预防和治疗必须花费的所有支出的普遍情形。投入是有成本的，而这些成本的总和取决于每种干预措施的对象锁定，这又决定了接受预防和治疗的人所占的总体比例。

　　预防措施的组合还可能包含疫苗接种，从而在模型中增加免疫状态。又或者，治疗不会促进康复，但会避免死亡。此外，对于介体传播的感染，预防措施可以采取更多形式。例如对于疟疾，我们可以通过躲避携带疟原虫的蚊子来保护人体：杀灭蚊虫，阻止蚊虫的孵化与成长，防止蚊子叮咬人体，包括让被感染者不被蚊子叮咬等。对任何此类因素的表述，都需要比公式（4）更复杂的模型。

　　所有这些情形都涉及如下任务：决定最优干预措施组合，以便从私人或社会的角度实现福利最大化（Gersovitz and Hammer，2004, 2005；Gersovitz，2010）。最优化的一阶条件直接明了，但仍有一些技术问题。一个问题是，即使假设干预措施的边际收益递减，动态最优化的充分二阶条件仍不能满足。此外，即使对非常简单的仅有一种干预措施的最优选择模型，在社会问题和私人问题上仍可能出现多重最优稳态。戈德曼和莱特伍德（Goldman and Lightwood，2002）等人分析过治疗的情形。涉及最优化问题的模型的多重稳态不同于不涉及最优化的动态系统的多重稳态。例如公式（3）的反复感染模型的最优化会产生二维动态系统，有一个状态变量和一个共态变量，但由于求最优解的要求，该系统不能循环运转（Skiba，1978；Grass et al.，2008）。

　　与有关疫苗政策的讨论相同，由于个人决策并不考虑社会后果，社会解与私人解是不一致的。对此的核心直觉是，人们若在被感染群体中停留时间过长，会给其他人造成危险（Gersovitz and Hammer，2004）。之所以如此，是因为人们太容易加入被感染群体，或没有足够努力脱离该群体。因此，涉及预防和治疗的选择都反映了外部性的影响。感染后的状态转化决定了应把干预内部化。例如在基于公式（4）的反复感染模型中，最优结果是给预防和治疗都提供补贴并采取相同比率，因为个人在预防和治疗方面都不会做得太多，而且程度也不相同。然而，当状态转化是从感染到死亡的时候，即使不考虑保险缺陷等因素，仅根据外部性也意味着应该给预防提供补贴，而对治疗征税（Skā- tun，2003；Gersovitz and Hammer，2004）。在现实中，对疾病折磨和死亡进行补偿的保险总是不完全的，因此上述发现没有多少政策意义，但能帮助我们理解隔离的外部性的理论本质。（⑥在这方面，经济流行病学研究文献主要采用了线性目标函数，使保险的问题能够得到巧妙处理。Gersovitz and Hammer（2005）的一项研究利用的效用函数，让非健康品支出的边际效用递减，但采取完全保险的假设。现有研究还没有采用非完全保险的完全状态依存函数的先例。） 至于介体传播的疾病，对预防的补贴比率取决于预防的类型，一种类型是对那些治疗可以帮助人们康复的传染病，应按照与治疗相同的比率为预防提供补贴（Gersovitz and Hammer，2004）。所以，干预措施的设计很大程度上取决于状态转化，但与对象锁定的类型无关（有关分析见Gersovitz and Hammer，2004）。

　　在反复感染模型中，如果感染的成本提高，社会计划者的最优稳态感染率就会下降。如果贴现率上升，最优稳态感染率就会提高，因为降低感染率要求更多地投资于健康干预，而回报是在将来逐步实现的。干预价格的提高对感染率的影响较为复杂，至少是源自某些直觉能发现的原因。考虑如下情形：我们必须做一定数量的某种干预但不能做更多，同时可以选择另一种干预的数量。此时，前一种（受限制的）干预行动的价格提高等于增加感染的成本，随着另一种干预的投入以最优化的方式增加，社会最优的感染率就会下降。另外，我们可以假设价格提高的某种干预措施在数量上是可变的，但它是唯一可行的干预选择。此时，干预行动价格提高的直接效应是减少其使用，从而导致感染率的净提高。在决定行动反应时，对象锁定的形式也会产生影响（Gersovitz and Hammer,2004）。

　　从理论上讲，政府可以通过税收与补贴的传统策略把外部性内部化。然而如上文所述，在实践中有大量预防和治疗行为难以观察，不能实施征税或补贴，例如在性传播疾病中过于私密的行为。这种情况提出了次优问题，尤其是当预防或治疗手段出现改进的时候。

　　流行病学家担心，当预防或治疗手段改进后，人们会放松对传染病的预防和康复的努力程度，他们将该现象称为“抑制解除”（disinhibition）。抑制解除的效应可能非常强大，反而导致感染率上升。不过，流行病学家的关注点不在于此类变化的综合福利影响（包括对预防与治疗的成本的效应），他们也没有区分最优策略得到实施或没有实施的情况，而这从福利角度看非常重要。经济学家担心的则是，当外部性没有得到纠正时，看似不错的创新反而可能导致福利下降，即所谓的贫困化（immiserization）。该原理的一个特定应用场景是：预防和治疗的创新可能导致贫困化，但需要什么条件？

　　我的一项研究考察了抑制解除和贫困化问题，对基于公式（4）的反复感染模型做了调整，使函数α和β不仅取决于各自的投入，还取决于函数中表示技术进步的一个移位参数（Gersovitz，2010）。在社会计划者把外部性内部化的时候（即采取社会最优策略），预防或治疗的技术改进都不可能导致贫困化。即使感染率上升，在考虑感染的全部影响（包括预防和治疗的成本）后，人们的福利水平依然会得到提高。

　　该研究显示，如果感染的外部性没有（或不能）通过最优补贴实现内部化，造成贫困化的一个必要条件是：抑制解除的效应非常强大，使感染率在技术进步之后出现提高（Gersovitz，2010）。对于不会使相关健康投入的边际产出a降低的预防技术改进，这种极端的抑制解除效应不可能出现。对这一结论的直观解释是，预防技术的改进会增加人们保持不受感染的概率，从而提高未感染状态的价值。所以在考虑了预防或治疗水平的所有内生调整之后，感染率仍会下降。可是治疗技术的改进却会降低未感染状态的价值，因为在感染后康复、回到未感染状态变得更加容易。即使投入的边际产出b与治疗技术改进彼此独立，在两种对象锁定情形下，治疗的改进仍会导致感染率提高，并可能导致贫困化。这两种情形分别是：（a）预防的对象锁定是未感染者；（b）预防的对象锁定是所有人，且易感染者所占比例超过50%。不过我的研究还提到了特定的函数形式α(a)和β（b)，使上述对象锁定情形不会导致感染率提高（Gersovitz，2010）。托克斯瓦尔德（Toxvaerd，2010a,b）的研究同样考察了次优选择问题。拉克达瓦拉等人（Lakdawalla et al.，2006）则针对那些会导致死亡而非康复的疾病，分析了贫困化现象。当然，这一问题并非他们的主要关注点，我们有必要研究能否拓展其分析思路，以找出此类传染病出现贫困化结果的条件。