*Mark Gersovitz, 约翰·霍普金斯大学经济学系教授,主要研究方向为发展经济学、对穷国经济的研究,其长期感兴趣的研究领域包括:储蓄行为与资本市场、农业、公共财政、国际商品市场以及卫生。目前正在进行的研究包括基于理性选择的传染病行为分析;穷国的税收,尤其是税收与企业规模分布的相互作用;以及非洲国家的内战。原文“The Economics of Infection Control”,发表于The Annual Review of Resource Economics,2011年,第3期,第277—296页。披露声明:作者没有对本文的客观性产生可能影响的任何隶属关系、会员关系、资助或财务关系。作者感谢伦敦帝国学院流行病学系与科罗拉多州立大学传染病研究集群为本课题提供的讲授机会,以及组织卓有成效的讨论。本文的部分内容取自如下研究成果:Gersovitz (2001),Gersovitz (2003),Gersovitz and Hammer (2003),Gersovitz and Hammer (2004)等。
1.引言
人们珍视健康,也珍视为实现特定健康水平而必须耗费的资源本可能获得的其他东西,还珍视某些有损健康的事物。因此,人们需要做出影响健康的选择,包括个人的选择与集体的选择。对此,一个好的或者说被经济学家认可的行为假设是:人们在特定约束条件下依据福利最大化原则做决策。
就传染病而言,流行病学与相关医学研究可以从传染生物学角度提供相关约束条件的信息。(①数理流行病学的卓越研究成果包括:Anderson and May (1991),Daley and Gani (1999),Diekmann and Heesterbeek (2000),Keeling and Rohani (2008),以及Ma and Li (2009)等。在下文中,若没有提及数理流行病学的具体引用来源,可以认为上述文献能提供便捷有效的指导。) 这些约束条件包括预防(含疫苗接种)以及治疗的选项及效果。此外,流行病学研究还能帮助理解传染机制,是人传人,还是通过中间宿主(像血吸虫病通过蜗牛),还是通过介体(像疟疾通过蚊子)等等。关键在于,对传染病的经济学分析应该基于数理流行病学的这些成果,否则会造成大量混乱、浪费和重复,并难以吸收他人的早期发现。
当然,流行病学不属于社会科学,并不涉及个人针对不同感染风险、不同预防和治疗选项及其成本如何反应的理论。流行病学也不涉及对策略和信息的考虑至关重要的行为理论,例如性伙伴之间试图评估彼此的风险程度,并根据情况采取相应行动等。流行病学同样不涉及因为个人最优选择与(通过政府的)集体最优选择存在矛盾而建立的公共政策理论,这是属于福利经济学的研究领域,特别是有关外部性的分析。(②流行病学家非常清楚,传染病的麻烦在于某个人的行为会影响其他人的福利,而且他们采用质量效应、社群效应或群体免疫(Fine,1993)等术语描述经济学家所说的外部性现象。这些概念同外部性概念的主要区别在于,经济学的外部性概念是基于理性个人独自行动的激励,不同于政策制定者从社会总体利益出发采取行动的激励。还有,政策制定者一方面会考虑个人对结果的评估,另一方面也认识到个人行为加总起来会影响人们的福利水平,但人们缺乏激励把这种影响纳入自身行动决策。此外,流行病学家的关注重点是群体免疫对消灭传染病的作用(Fine,1993),而非在通过干预措施改变传染病的流行程度时,如何权衡相关的成本与收益(Gersovitz and Hammer,2004)。) 上述课题均在经济学研究视野之内,因此对人类行为会如何影响传染病流行程度及其全部成本,政府对控制传染能发挥何种作用,经济学研究可以作为流行病学的有益补充,并做出巨大贡献。
经济学家在这一领域业已起步,本文将展示他们已取得的成就,以及在此过程中如何借鉴流行病学的发现,尤其是数学模型和数理流行病学的有关成果。作为研究主题的传染控制经济学理论是抽象的概念,但其最终目的是为现实决策提供指导。
2.模型的构成要件
为传染病设计控制程序,第一个任务是枚举人们所处的可能的健康状态。在最简化意义上,人们要么处于易感染状态,要么处于被感染并具有传染性的状态。而在现实中,人们可能已被感染但并不具有传染性。最简化的模型对后者未做区分,本文也是如此。人们可能处于免疫状态,因为曾经被感染并康复,或者因为接种了疫苗,或者具有自然免疫力。人们还可能受致命感染而死亡。模型的下一个任务是描述人们如何从一种健康状态转化为另一种状态。
2.1约束条件:从易感染者转化为被感染者
任何传染模型的核心,都是通过与被感染者的接触而产生新感染的机制。根据传染病的特征,数理流行病学总结出了很多描述公式(见脚注①)。
最简化的机制是一种所有人的行为方式都相同的人传人模型。具体而言,每个人在每次接触中遇到其他任何人的概率都相同,假如遇到的人是被感染者,则他们受感染的概率相同,另外每个人同他人接触的频率也相同,由此构成了一个同质性的随机匹配模型。形象地说,好比所有人都进入一个房间,与其他人有相同次数的握手,假如握手对象是被感染者,则可能受到感染。
基于上述假设,新感染的人数将由下列公式决定:
新感染人数 = αSπ(1)
易感染者每次接触(有传染性的)被感染者的概率为π,也就是被感染者人数(I)在总人口(N)中所占的比例(即总感染率),π = i = I/N,这对所有人是相同的。Sπ代表每次接触被感染者的易感染者的人数。α代表一个调节因子,包含接触率与被感染者的固有传染力。在基于公式(1)的数理流行病学经典简化模型中,通常只存在两种稳定状态:零感染稳态与流行病稳态。若模型纳入更多复杂因素,显然会出现多重流行病稳态或分叉结果,下文有相关案例介绍。
在数理流行病学中,α被当作外生于模型机制的固定参数来处理,然而对经济学家来说,该调节因子和其他参数都同个人与政府的选择有密切关系。这里的假设是,选择将取决于总感染率,因为后者会影响受感染的概率。菲利普森(Philipson,2000)称之为“行为的流行弹性”(prevalence elasticity of behavior)。
对某些传染病,需要用多组别模型才能充分描述感染过程,当然缺点是会增加分析的复杂程度。其中最简化的模型包含多个组别,每个组别有不同接触率,但所有组别的成员间做随机接触。接触率较高的组别在总接触人数中占比较高,也更容易受到感染。另外在每次接触被感染者时,人们受感染的概率也可能存在异质性。
在最简化的多组别模型中,相当于仍只有一个房间,人们在其中做随机接触,但不同组别的人的握手频率不同。此类模型的一个核心结论是,疾病的最终传染状态不仅取决于平均接触率,也与接触率的分布状况有关(Anderson and May,1991, 第 233页)。另外在此类模型中,不太活跃的组别的活动水平增加反而可以降低总体感染率(Whitaker and Rentin,1992; Kremer,1996)。由此看来,并非有风险活动的所有外部性都必然是负面效应。
在更复杂的多组别模型中,某些组别的成员与其他组别的成员以不同比率混合起来。例如可能存在多个房间,来自每一对组别的成员可能以特定比率进入特定房间,每个组别的成员可能以特定频率随机握手。西蒙等人(Simon and Jacquez,1992)深入探讨了此类结构化混合模型,重点关注稳态的稳定性。另有研究(Chen,2006b)考察了由个人在风险行为和有成本的安全行为之间做最优选择的多组别模型。还有学者(Huang et al.,1992)
提到的多组别模型案例的接触率取决于组别规模,而非固定的频率,此类模型可能得到有正感染率的多重稳态。可能导致多重传染稳态结果的模型在分析处理中很困难。对任何具体模型而言,是否存在多重传染稳态都是一个重要特征,需要尽可能深入理解并分析其影响。
多组别建模的第三种具体方法以两性别(twosex)建模为代表。当来自两个组别的人进入一个房间后,他们只同来自对方组别的成员接触,而不是同房间里的所有人随机接触。这种方式会带来供给需求问题:两个组别的相对人数和接触率结合起来,必须使来自A组别的人同B组别的人握手的需要,等于来自B组别的人同A组别的人握手的需要。更复杂的情形是,不同组别在某种致命疾病面前可能有不同的死亡率,因为不同特征或易感染性会使不同组别的人处于不同的风险水平。由此将导致在初期满足供需平衡的相对人数和接触率,随时间推移不再有效。
大量流行病学研究讨论了使需求能在流行病期间始终等于供给的组对规则(如Blythe et al.,1991)。关注贸易和补偿问题的经济学研究在这一领域也可以提供借鉴。大组别的人如果想更为频繁地同小组别的不想频繁接触的人握手,可以给第二组别的人付钱,以增加其握手频率。同时,前一组别的人的付款可能降低自己组别的握手需求。每个组别所做的这一利弊权衡,会使两个组别对握手的需求和供给达到平衡。这种流行病学模型起源于对性传播疾病的研究。近期对性交易的经济学分析设计了一个市场静态均衡,价格可发挥平衡供给与需求的作用(Edlund and Korn,2002;Rao et al.,2003;Gertler et al.,2005)。但为研究传染机制,此类模型必须置于动态架构之下。
最后,导致感染风险的接触类型未必需要人与人之间的直接接触。易感染者面临的风险可能来自空气中的病菌、污染的水源,或被感染的介体,而病菌与被感染介体的数量可能受实时动态系统中的人类总感染率的影响。这些过程都必须做专门的模型设计。数理流行病学对该领域的关注由来已久,可以追溯到20世纪头10年罗纳德·罗斯(Ronald Ross)爵士对疟疾的研究。
2.2约束条件:其他转化
从易感染者到被感染者的转化,是传染病导致的健康状态序列变化的一个中间阶段。序列的开始决定了易感染者的人数,人口增长则给易感染群体提供了重要的输入量。新生儿通常未被感染,但也有某些感染可能通过母亲传递给胎儿,或通过哺乳传递给新生儿。假如传染进程的作用时间较长,则需要考虑人口增长的因素。
模型是否纳入人口增长,可能对定性动态分析和政策启示有重要意义。例如有学者(Geoffard and Philipson,1996, 第604页)在讨论不包含出生和死亡的固定人口艾滋病模型时总结说:“感染率提高与公共补贴对保护措施的引入形成拉锯作用,这使公共干预的时机成为决定其经济效率的关键因素,如果补贴的实施不够迅速,则普遍感染会使其对保护措施的促进作用失效。”这一表述似乎在说,假如政府干预被延误太久,再采取任何措施都将没有意义。然而,即便政府行动有所延误,感染率高于政府应该通过补贴来限制其达到的水平,这种情形也只会是暂时现象。随着新出生(或新的性活跃)人群进入易感染者的队伍,政府仍可以引入更多预防措施,把感染率拉回社会最优水平。因此,上述总结只是在未考虑易感染人群的新加入人口时才成立。本文第3节还将有更多案例来介绍考虑了新加入者后的重要影响。
从易感染者向被感染者转化之后,根据传染病的特性,还会有其他转化过程。生物学上有几种符合常识的可能结果:被感染者可能长期维持被感染状态,但对其寿命没有特别影响;可能康复,并再次受到感染,也叫作“反复感染”(susceptibleinfectedsusceptible infection,SIS),这些人经常处于易感染或被感染的循环中,与新生儿一样成为易感染人群的新输入量;被感染者可能在康复后具有免疫力;或者致命传染病可能导致人们死亡,等等。当然也存在多种情形混合的情况,如某些被感染者可能康复,某些可能死亡。与人口增长的情形相似,感染后的转化状态对政策有重要含义,这将在第3节中阐述。
感染后的状态转化对模型的数学处理也很关键。在最简化模型中,要么(a)没有新生儿,如果人们不再处于被感染状态,就会康复并具有免疫力,而且不会死亡;要么(b)可以有新生儿,人们在易感染和被感染之间循环,可能死亡,但不是因为感染本身死亡。对前一种情形,模型可能得出某些解析解(如Francis,1997, 2004;Boulier et al.,2006)。对后一种反复感染的情形,模型只能求解出一种相关的状态,即易感染者所占的比例(或者被感染者所占比例,二者之和为1),这是个重要的简化结论。
对于其他状态转化假设,哪怕是用最简单的同质性随机匹配方式,也会得出更难处理的多状态模型。例如,人们可能因为染上传染病而死亡,但在对艾滋病一类的致命疾病建模时,研究者容易忽略死亡因素,因为模型可以把人口总规模视为内生,这等于加入了一个状态变量。吉奥法德和菲利普森(Geoffard and Philipson,1996)在分析艾滋病时就假设,感染会提高个人的贴现率,但不会导致人口减少。另外有学者在研究艾滋病变化机制时也未考虑其致命特征(Chen,2006a,b;Chen and Cottrell,2009)。这样建模虽然容易做数学处理,却没有包含艾滋病的关键性质。我们应抵制这种做法的诱惑,因为它严重违背现实,有关论述另见下文。
2.3约束条件:干预的可行性
生物医学上的约束条件决定了人们能如何防范感染,以及在被感染之后如何加以应对。在人传人的感染中,干预措施包括各种预防措施和治疗,视具体疾病的情况而定。如果可行,疫苗是关键的预防办法。在某些情况下,需要用测试来获知某人是否受到感染。菲利普森等人(Philipson and Posner,1995;Mechoulan,2004)分析了理性决策者对测试的态度,我(2011)对艾滋病测试做了调查。其他干预措施还包括:(a)在感染存在潜伏期的时候,对可能已被暴露的人实施观察隔离;(b)对确认的被感染者实施隔离。
从行为角度看,干预措施的一个重要方面在于个人或社会总体上能否掌控这些措施。隔离或观察隔离可以由政府强制执行,可以迫使个人遵守,而人们可能成功地逃避隔离约束。不过对大多数干预措施而言,最终决定权显然在个人。预防和治疗措施经常涉及私密行为,难以被监督。即使在理论上可以监督,这些行为可能也过于频繁和分散,使政府只能发挥间接影响。例如政府可以通过补贴洗手液间接鼓励洗手,却不能给洗手本身提供补贴。这些现象对干预措施的实施以及本文第3节要讨论的次优理论有重要含义。
2.4干预措施的对象锁定
对象锁定决定了哪些人能得到预防和治疗等干预措施。无论对社会计划者还是个人决策者而言,这是介于约束条件和选择之间的因素。我们可以设想出多种安排,其中某些有更大可能性。在理想状态下,我们可以明确考虑识别干预对象的可行性与成本。例如,找到需要治疗的被感染者就是公共卫生主管机构的当务之急,并应该明确纳入模型。另一个例子是接触追踪。但就我所知,目前得到最多研究的只是分析某些对象锁定的选项及其定性含义(Gersovitz and Hammer,2004;Gersovitz,2010)。由此看来,对象锁定更像是约束条件,而非自由选择。
假如对象锁定不花费成本,最理想的预防对象锁定应该只面向不一致的匹配,即未感染者与被感染者的接触。与之类似,治疗的最佳对象锁定应该只面向被感染者。而在现实中,各种类型的对象锁定都是有可能的。公共卫生部门有时采取普遍的治疗对象锁定策略,在难以分辨谁受到感染、治疗成本相对较低、治疗的副作用不严重的情况下,面向所有人实施。预防措施除面向不一致匹配外,也可能面向未感染者、被感染者乃至所有人实施。
2.5目标设定
经济学研究视角意味着,对传染病的后果及干预方法应开展全面的、以效用为基础的测算评价。传染病控制不能以感染率为唯一目标,根除疾病等结果也必须结合相关的全部成本和收益来评价。目前采取的行动会有直接的成本和收益,但也会对未来的成本尤其是收益产生影响。对未来产生的成本和收益,有充分的理由做贴现计算。无论是个人还是政策制定者,在决策时都必须对全部成本和收益加以权衡,并预测未来的成本和收益,而这些又取决于未来的感染率变化路径。上述考虑意味着以效用的当前贴现值为目标,变量的未来取值基于和同一模型产生的未来场景相一致的理性预期,否则,可能存在把外部性等市场失灵混同于短视决策的危险。即使对理性预期的现实性存在疑问,在说明公共政策的合理性时,我们仍有必要区分外部性造成的影响同错误信息或短视造成的影响。少数学者还单独分析了预期和信息获取发挥的作用(Auld,2003;Chen,2009),奥尔德尤其关注了悲观主义预期的情形。
在任何时候我们都应该考虑到,一个人的福利状况还取决于(保险赔付之外)支付预防和治疗费用后剩下的用于其他产品的收入。因此,用于预防和治疗的资源每增加一点,都会挤占其他用途的资源。一个人是否被感染,以及感染是否妨碍工作
可能会影响这个人的实际收入。如果预防措施需要回避有危险的工作活动,也会直接压低收入水平。另外,大多数人或许认为,某个人的福利状况首先取决于感染造成的直接后果,如疼痛、折磨和恐惧等,其次才是感染的间接后果,如对收入的影响等。所以对目标的最佳描述或许是一种状态依存效用函数,使福利水平直接取决于是否受到感染,并使减去健康支出的净收入的效用(和边际效用)非常灵活地同感染状态挂钩。为便于数学处理,还可以采用其他更简单的效用函数表述。可见,在设定传染控制的目标函数时有大量考虑因素,而且不可避免地需要在基于概念的最佳理论建模同数学处理的要求之间权衡取舍。模型的简化处理或许有帮助,但必须充分考虑到相应的影响。
对社会目标而言,最佳办法是设法把人们对自己状况的评估值加总。这种加总或许是累加式的(功利主义方法),或许要采用另外的社会福利函数。成本收益方法则不应该采用,因为该方法回避了对健康结果的价值评估,完全不能解释某些活动为什么应具有公共性质而非私人活动,其政策建议也不是根据外部性及其他市场缺陷(Gersovitz and Hammer,2003)。
总之,在设计传染控制模型时,有许多因素需要斟酌。生物医学方面的考虑是这种多样性的一个重要成因:对不同传染病需要做不同设定。不同设定则会对模型的数学处理有重要影响。所以总体上看,关于传染病控制的研究将产生多种类型的模型,从适合某种传染病的模型中得到的启发,在借用于其他疾病的研究时应保持谨慎。下面将把以上讨论的组成部分拼接成模型,以回答通过干预措施的设计来控制传染病的某些问题。当然,现有经济学研究文献远没有形成完善的模型类型。
3.模型的构建与运用
3.1外部性:对传染加以公共控制的主要动机
当人们出于自利做出个人决策时,他们只会考虑直接影响自己的因素。他们对预防和治疗的选择会考虑自身(或许还有较为亲近的人)的收益与成本,但不包含其他人的收益与成本。由于每个人都只是群体中的一员,各人的决策对传染病的总体变量仅有极微小的影响,所以各人不会考虑自身决策导致的传染病变化再产生的影响。可是个人的决策加总起来,却会导致传染病的流行,人们的决策加总起来会对其他人的福利产生作用,形成感染的外部性。因此,个人的决策未必是社会最优结果。经济学家沿着外部性思路采用的理论概念,也就不同于流行病学家采用的羊群效应、质量效应或社群效应等说法。
对于私人激励与社会激励的差异,福利经济学的解决方案是对具有利他福利效应的个人行为提供补贴,而对损害他人利益的个人行为征税。由此继续让个人做决策,但其激励会有所调整。本来不在自己考虑范围之内的社会后果,通过补贴或税收的干预,将内化为个人自己关注的内容。
从机制上讲,测算这种补贴或税收体系的一种办法是三阶段操作:第一阶段,假设社会计划者可以实际控制健康方面的所有决策,通过目标函数(通过对众多个人福利水平的某种测算)的最大化测算出社会最优水平。最重要的一点是,社会计划者会考虑决策对传染病总体发展的影响,这种测算通常由不同学科的应用控制理论家(包括流行病学家)完成,针对不同感染场景,并有悠久历史(Wickwire,1977;Sethi and Staats,1978;Wiemer,1987)。第二阶段,测算出个人在最大化其目标函数时的行为选择,但不考虑对传染病的总体影响。第三阶段,测算出要让个人决策等同于社会计划者的选择,使社会计划者测算出的理想结果能分解到个人决策者,应该在第二阶段安排多少补贴或税收。后两个阶段的操作是福利经济学方法的真正标志,较少得到应用,并且很自然地只是由经济学家采用。(③有学者设计的模型让面临感染风险的决策者做最大化选择(Chen,2004;2006a,b;2009;Chen and Cottrell,2009),以此考察参数变化对感染率的影响,但不涉及对决策者福利的影响,也未讨论如何能对个人激励加以调整,使其采取社会最优水平的决策。) 本节其余部分将介绍开展此类三阶段分析的现有成果。
当然,以上关于约束条件的讨论(第2.1节到第2.4节)中提到,对于传染病采取此类补贴或税收干预未必可行,至少有时不能直接针对社会和私人的成本收益差异。假如没有看到这一事实,没有对模型做相应扩展,则可能导致外部性概念变成一个很模糊的比喻,而不能给实际干预措施的设计提供真正借鉴。例如在性传播疾病中,我们不能对有风险的性行为本身征税,而这在理论上是社会计划者解决方案实施的目标所在。并且与依靠信息采集技术的进步、通过收费来控制交通拥堵和污染的伦敦交通区划方案不同,上述事实显然难以通过监督技术的改进予以克服。对许多健康相关的行为而言,征税或补贴的困难源于其内在本质,技术革新不足以解决问题。我们可以对购买避孕套提供补贴,但这一补贴不等同于给在危险性行为中使用避孕套提供补贴,人们不可能也不愿意直接监督后者。无论如何,免费发放避孕套或许仍不足以使其达到最优使用水平,甚至花钱请人们取走避孕套也不等同于就能使其得到利用。当社会计划者的最优解决方案出于此类原因无法实施时,表面上合意的选择反而会使情况变得更糟,给我们提出次优选择问题。
外部性理论在疫苗上的应用,给许多类似问题提供了一个很好的案例。如果能找到疫苗,它将是一种关键的生物医学干预手段。疫苗的建模相对简单,至少对一阶近似是如此,因为这是一个二选一的决策。对疫苗政策的分析可以具体揭示如何把传染病控制模型的各个部分组合起来。对人们是否遵从干预措施可以做较好的监督,因为疫苗接种是由专业医疗人员完成的。另外尽管必须配合接种,但如果获得免疫力只需要一次注射,则不需要更多的服从配合。对疫苗接种的研究充分揭示了外部性对激励政策的影响。但事实上,某些学者认为在疫苗问题上,并不存在外部性导致的公共政策合理性。对这一观点的考察非常有益于我们了解感染的外部性的本质。
3.2疫苗接种模型
给人们提供传染病疫苗接种的公共计划经常被作为用政策克服外部性的绝好案例,这是因为人们通常不会考虑自身获得免疫力后,不再会感染他人带来的收益。然而菲利普森(2000,第 1763—1764页)不同意这一基于外部性的说法:
的确,根据对疾病预防的正外部性的正统观点,经济学家通常支持对传染病预防采取积极的公共行动……然而,他们很少尝试去解释疾病发生模式,或者在个人根据约束条件做出最优决策的社会中对公共干预效果加以评估。近期开展的此类研究则质疑了经济学古老教科书中的观点……
弗朗西斯(Francis,1997)在考察疫苗接种时,首次对传染病控制做了规范的动态分析,把社会最优与私人最优做对比,以考察外部性的本质。他强调,如果有任何组别给易感染者造成外部性,那是来自被感染者,而非未接种的易感染者。因此他指出,需要把从易感染者到被感染者的转化明确纳入动态模型,才便于理解外部性,这也表明芬恩和克拉克森等人(Fine and Clarkson,1986;Brito et al.,1991;Xu,1999;Kureishi,2009)的研究采用静态分析方法有其不足之处。
不过在弗朗西斯(1997)的模型中,并不存在外部性,或者说不存在证明需要政府干预的外部性。实际上,他的假设似乎是有意识地为激发未来的研究而设计的。他假设,不存在无感染和无免疫力的新生人口,因此易感染人群没有这一输入量;另外没有人从感染中康复,也没有人因为任何原因死亡。这套关于健康状态转化顺序的假设成为其结论的核心。在弗朗西斯的模型中,成本和收益都是贴现值,如果感染率较低,疫苗接种的即期收益也就较低,所以把疫苗接种的成本推迟就是值得的。
我(2003)之前对弗朗西斯的上述结论做过如下直觉描述:如果没有新生和死亡,也无人接种疫苗,则感染会扩大——如公式(1)的描述——因此易感染者所占比例会持续下降,被感染者所占比例持续上升。随着被感染者比例的上升,剩余易感染者被感染的风险将增加,通过疫苗接种获得免疫力的收益也会提高。最终,被感染者所占比例(感染率)会达到一个临界值,使接种疫苗的收益等于接种疫苗的成本(后者为常数)。无论是从社会还是个人视角看,如果任何人接种疫苗是值得的,那么对所有易感染者接种疫苗也都是值得的,因为如果不这样做,被感染者所占比例(以及易感染者被感染的概率)仍会继续提高。总体感染率不可能下降,因为没有新出生的易感染者,没有被感染者的康复或死亡,这些都是关键的状态转化假设。此时,让感染率维持稳态水平的唯一办法,就是一旦达到临界值后对所有易感染者接种疫苗。因此在稳态情形下,易感染者所占比例为零。
由于临界值对社会行动与个人行动而言是相同的,就不存在外部性,至少不存在表明需要干预措施的外部性。或许有人会推测,政府可能希望把临界值设定在更低水平,以更早达到。但为什么要这样做呢?政府为了使感染率达到临界值,需要给所有人接种疫苗,因此没有易感染者会因为感染率的不再提升而受益。换言之,一旦达到私人临界值,每个人反正都会接种疫苗,而如果每个人都会接种,也就不会有人因为降低总感染率而提前接种并由此获益。所以政府提前给所有人接种疫苗并无意义,政府和私人的临界值是相同的。
我之前的研究分析了如下情形,有新出生人口,有死亡人口,但死亡人数仅为现存人口的一定比例,任何组别的人都呈渐进式死亡,这是数理流行病学中为数学处理而采取的很传统的假设(Gersovitz,2003)。上述关于出生和死亡的假设是与弗朗西斯模型(1997)的唯一不同之处,关键在于,依旧假设被感染者从来不会康复。
假如政府像社会计划者那样采取行动,可以控制谁接种疫苗,它将最大化汉密尔顿函数的现值(Gersovitz,2003):
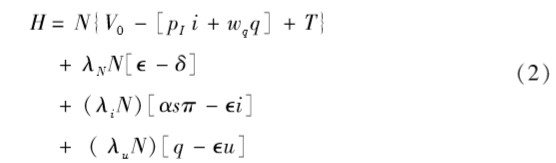 |
公式(2)的第一行是社会计划者的目标:V0是某人在无感染情况下的效用的货币价值,pI是受到感染造成的成本(因此这一目标比有非健康产品支出的状态依存效用函数更简单),i是所有N个人中被感染者所占比例,wq是包含所有税收或补贴在内的疫苗接种的成本(对社会计划者而言,等于实际发生的成本pq),q是所有N个人中目前被接种者所占比例,T是因为wq与pq的差异而发生的税收或补贴总和(对社会计划者而言,为0)。公式的第二行是附加拉格朗日乘数λNN,表示总人数N的变化,其中为出生率,δ为死亡率。第三行是附加拉格朗日乘数λiN,表示感染者所占比例i的变化,其中对社会计划者而言,π = i;s是易感染者所占比例;α与公式(1)中的含义相同。第四行是附加拉格朗日乘数λuN,表示曾经接种疫苗且目前仍存活者所占比例u的变化。请注意:i+s+u=1。
公式(2)的汉密尔顿函数可以推导出社会计划者实施疫苗接种最优策略所需的标准条件。最优解确立了一个由疫苗接种维持的稳态感染水平,不是所有易感染者都会获得接种。如果认为稳态情况下的最优选择是对每个人都接种,则会导致矛盾。因为若采用普遍接种策略,对所有新出现的易感染者接种,则会稀释被感染者在总人口中所占比例,把感染率降低到稳态水平之下,而这一结论与在稳态感染率水平上每个人都接种疫苗的概念相悖。因此社会计划者的最优策略是对
一定比例的易感染者接种疫苗,该比例严格小于1,一旦达到稳态感染率,则继续对包括新生人口在内的易感染者实施部分接种,并使易感染者、已接种者和被感染者所占比例保持不变。
对于典型的个人,可以理解为同社会计划者一样用公式(2)的汉密尔顿函数来决定何时接种疫苗,只是个人把π视为外生因素(尽管由于其具有典型性,π应该等于i)。另外,如果政府对接种疫苗提供补贴,以比率tq<0把最优决策做分散化处理,则有(wq-pq) = tqpq,而且T不等于0。典型的个人最优决策还涉及稳态感染率,但如果没有干预,则不同于政府的目标。没有政府干预时,私人临界值会高于社会临界值,因为前者未包含对其他人受感染的总体概率的影响。当政府对最优稳态做分散化决策处理时,会对疫苗接种提供补贴,并做如下设定:
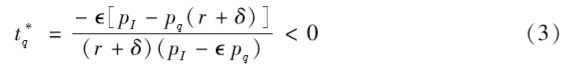 |
事实上,出生人口给总人口带来了异质性:不是所有人都生活在同一时刻,未出生的人也不能与已出生的人一起做决策。只要出生率为正,无论其是否超过死亡率,无论总人口增长是否为正,都会得到补贴为正的结果。
我之前的研究还表明,如果被感染者康复后再度成为易感染者,康复可能起到与正出生率类似的作用,导致外部性,给政府干预提供理由,得出与公式(3)类似的推导结果(Gersovitz,2003)。与人口出生和死亡的问题相似,同弗朗西斯模型(1997)的主要区别在于是否存在向易感染人群转化的假设。在两种情形下,补贴的绝对值都负向取决于疫苗接种的成本和利率,正向取决于感染的成本,但与转化参数α完全无关。补贴的绝对值正向取决于出生率,在前一情形中负向取决于自然死亡率,在后一情形中正向取决于康复率。
在这两个模型中,政府干预的目标都是通过降低疾病流行水平,提高福利。只有当感染的成本无限大,或疫苗接种的成本为零时,政府的最优稳态感染率才会等于零,使传染病被完全消灭。但这只能是渐进的形式,因为被感染者人群只会逐渐消失,每个时期只有固定比例的被感染者死亡或康复,这是为数学处理而设定的假设的结果。还有,在感染成本无限大或疫苗接种成本为零的情形下,政府稳态与私人稳态重合,而且由于稳态感染率都是零,彻底消灭传染病并不需要政府的干预。
弗朗西斯与布里埃等人(Francis,2004;Boulier et al.,2006)的研究提供了更多关于外部性与疫苗接种的例子。在他们的模型中,人们的健康状态可以从易感染者转化为:(a)若接种疫苗,成为已接种并免疫的状态(布里埃等人的研究中允许出现疫苗接种失败);(b)被感染后康复的状态。没有贴现,因此接种疫苗的任何人都是在传染初期被接种,但弗朗西斯设置了一个(有能力约束的)疫苗接种最大比例;也不存在人口出生和死亡。这些假设是特定的,但对于相比利率、出生和死亡来说进程较快的传染病,或许是较恰当的近似描述。这两篇论文的主要关注点都是季节性流感,而且作为求解技巧做了一个附加假设,即传染病在最优化期限内(当t=∞)会接近稳态。不过即使对季节性流感等疾病而言,该假设仍存在争议,因为我们不能假定流感季节结束正好是对应模型的稳态趋近,而非随着天气或人们行为的变化导致感染出现季节性减少。
还有研究提出了另一套假设条件(KribsZaleta and VelascoHernandez,2000),模型采用固定的疫苗接种率,但如果疫苗只是部分有效,会导致多重稳态结果。该模型中存在人口出生和死亡(但不是由感染本身导致),出生始终等于死亡,所以不存在人口净增长。人们会从感染中康复,再次成为易感染者,疫苗只能提供部分免疫力,免疫力随时间递减。疫苗接种率不是最优决定的,因此接下来的问题是:如果对多大比例的人进行疫苗接种做出最优选择,稳态是否有唯一解。后来的研究(Chen,2006a;Chen and Cottrell,2009)考察了与上述相似的模型,但假设人们在感染后不会康复,个人做最优化决策,仍会在这些条件下出现多重稳态的结果。不过后来这些研究未考察社会计划者的问题,也就没有发现外部性。布里埃等人(2006)的研究同后面两篇论文在多重稳态方面的结论差异或许在于,布里埃等人的最优化是在期初完成,而且由于人口不存在流入和流出,疫苗接种不需要持续开展。
我们做个对比:以上研究的结论是通过补贴把传染病控制在一定水平,但不是彻底消灭;而吉奥法德等人(Geoffard and Philipson,1997, 第 222页)则认为,由于无法根除传染病,“通过庇古税类型的补贴解决因为正外部性而供给不足的疫苗接种问题,这一经典理由应值得商榷”。(④在Geoffard and Philipson(1997)的模型里,人口的一定比例会死亡,这使任何组别都不会在有限时间内全部死亡,因此该模型中的疾病消灭最多是渐进式的。此外,他们在疫苗需求的异质性假设之下没有提供关于消灭传染病的社会最优结果,故难以将其结论同我的研究(Gersovitz,2003)做直接比较。最后,在假设疾病可以在有限时间内消除的关于根除疾病的简短讨论中,他们没有分析消灭疾病在何时是最优解,而只是对其成本和收益的上限和下限做了较弱的分析(Geoffard and Philipson ,第227页)。 )其实,根除传染病的政策并不意味着通过补贴最优化地抵消外部性的政策。相对于收益而言,根除疾病的代价可能过高,但仍有充分理由通过最优化的疫苗接种补贴来减轻传染病的流行程度。而且根据那些假设感染只会渐进式消失的现有模型,当根除疾病在有限时间内可行时,首要研究任务之一仍是对疫苗接种做建模分析。(⑤Barrett and Hoel(2007)讨论了在有限时间内消灭传染病的情形,但其模型设定存在疑问。如果被感染者是终生携带者,则在目前的所有被感染者都死亡之前,疾病不可能完全消灭,而描述疾病消灭可能需要叠代模型。假如人们可能康复,则疾病消灭至少要求足够的时间,使最后一名被感染者康复或者死亡。这些是细微的必要条件,在有限时间内消灭疾病的模型必须将它们纳入考虑。然而Barrett and Hoel的模型设定并未明确,受感染的每一个人将如何在有限时间内死亡或康复,以及如何能实现疾病消灭。他们在其文献的第631页引入了公式(3),似乎是作为在有限时间内死亡或康复模型的替代机制,并将疫苗接种作为唯一的干预手段。但根据我对此问题的理解,这种模型设定缺乏从一种健康状态到另一种健康状态(易感染者、被感染者、康复者、免疫者、被接种者、死亡者等)的流行病学转化机制基础,以实现有限时间内的疾病消灭。尤其是,该公式似乎意味着疫苗接种会直接让人们脱离被感染者(而非易感染者)群体,因此也有与Francis(1997)的研究类似的谬误。)
在这一阶段,弗朗西斯与菲利普森(Francis,1997;Philipson,2000)的研究对疫苗接种外部性理由的反对,除一个不能广泛适用的案例外,似乎不具有普遍性。他们的观点更多是出于学术探讨,是对未来研究的启发,而非政策指导。当然,要描绘与疫苗接种有关的外部性影响的全貌,还需更多努力。
3.3更普遍的预防与治疗模型
在人们可以阻止传染的预防行动中,疫苗接种只是一个选项。另外,被感染者还可以接受治疗。对于通过随机同质性匹配实现人传人、被感染后不能康复或康复后可能再度被感染的反复传染(SIS)疾病,被感染者的比例将由如下公式决定:
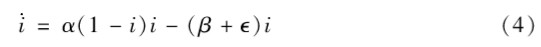 |
对这一数理流行病学重要公式的推导,可参见我和哈默(Gersovitz and Hammer,2004)的研究。上式右侧的第一项对应公式(1)中用比例π=i表示的新感染者;第二项表示康复后重新成为易感染者的比率β,和新出生后成为易感染者的比率ε。
预防和治疗选项的自然表述是让α与某种预防投入a挂钩,该投入的增加会降低α的数值,另外使β与某种治疗投入b挂钩,该投入的增加会提高β的数值。与大多数研究文献不同,这一设定不是要么做要么不做的选择,而是让投入成为一个连续变量,这种性质能对应医疗支出的广泛区间变化,并具有边际收益递减的特征。除贴近现实外,该假设还为最优化问题提供了凹性函数基础,尽管仍不能保证问题可以求解。这种设定不同于从患者内省(意即让人们自己出去找到一个处方,为其付款,并遵照执行)中产生的僵化假设,更能代表为实现类型广泛的预防和治疗必须花费的所有支出的普遍情形。投入是有成本的,而这些成本的总和取决于每种干预措施的对象锁定,这又决定了接受预防和治疗的人所占的总体比例。
预防措施的组合还可能包含疫苗接种,从而在模型中增加免疫状态。又或者,治疗不会促进康复,但会避免死亡。此外,对于介体传播的感染,预防措施可以采取更多形式。例如对于疟疾,我们可以通过躲避携带疟原虫的蚊子来保护人体:杀灭蚊虫,阻止蚊虫的孵化与成长,防止蚊子叮咬人体,包括让被感染者不被蚊子叮咬等。对任何此类因素的表述,都需要比公式(4)更复杂的模型。
所有这些情形都涉及如下任务:决定最优干预措施组合,以便从私人或社会的角度实现福利最大化(Gersovitz and Hammer,2004, 2005;Gersovitz,2010)。最优化的一阶条件直接明了,但仍有一些技术问题。一个问题是,即使假设干预措施的边际收益递减,动态最优化的充分二阶条件仍不能满足。此外,即使对非常简单的仅有一种干预措施的最优选择模型,在社会问题和私人问题上仍可能出现多重最优稳态。戈德曼和莱特伍德(Goldman and Lightwood,2002)等人分析过治疗的情形。涉及最优化问题的模型的多重稳态不同于不涉及最优化的动态系统的多重稳态。例如公式(3)的反复感染模型的最优化会产生二维动态系统,有一个状态变量和一个共态变量,但由于求最优解的要求,该系统不能循环运转(Skiba,1978;Grass et al.,2008)。
与有关疫苗政策的讨论相同,由于个人决策并不考虑社会后果,社会解与私人解是不一致的。对此的核心直觉是,人们若在被感染群体中停留时间过长,会给其他人造成危险(Gersovitz and Hammer,2004)。之所以如此,是因为人们太容易加入被感染群体,或没有足够努力脱离该群体。因此,涉及预防和治疗的选择都反映了外部性的影响。感染后的状态转化决定了应把干预内部化。例如在基于公式(4)的反复感染模型中,最优结果是给预防和治疗都提供补贴并采取相同比率,因为个人在预防和治疗方面都不会做得太多,而且程度也不相同。然而,当状态转化是从感染到死亡的时候,即使不考虑保险缺陷等因素,仅根据外部性也意味着应该给预防提供补贴,而对治疗征税(Skā- tun,2003;Gersovitz and Hammer,2004)。在现实中,对疾病折磨和死亡进行补偿的保险总是不完全的,因此上述发现没有多少政策意义,但能帮助我们理解隔离的外部性的理论本质。(⑥在这方面,经济流行病学研究文献主要采用了线性目标函数,使保险的问题能够得到巧妙处理。Gersovitz and Hammer(2005)的一项研究利用的效用函数,让非健康品支出的边际效用递减,但采取完全保险的假设。现有研究还没有采用非完全保险的完全状态依存函数的先例。) 至于介体传播的疾病,对预防的补贴比率取决于预防的类型,一种类型是对那些治疗可以帮助人们康复的传染病,应按照与治疗相同的比率为预防提供补贴(Gersovitz and Hammer,2004)。所以,干预措施的设计很大程度上取决于状态转化,但与对象锁定的类型无关(有关分析见Gersovitz and Hammer,2004)。
在反复感染模型中,如果感染的成本提高,社会计划者的最优稳态感染率就会下降。如果贴现率上升,最优稳态感染率就会提高,因为降低感染率要求更多地投资于健康干预,而回报是在将来逐步实现的。干预价格的提高对感染率的影响较为复杂,至少是源自某些直觉能发现的原因。考虑如下情形:我们必须做一定数量的某种干预但不能做更多,同时可以选择另一种干预的数量。此时,前一种(受限制的)干预行动的价格提高等于增加感染的成本,随着另一种干预的投入以最优化的方式增加,社会最优的感染率就会下降。另外,我们可以假设价格提高的某种干预措施在数量上是可变的,但它是唯一可行的干预选择。此时,干预行动价格提高的直接效应是减少其使用,从而导致感染率的净提高。在决定行动反应时,对象锁定的形式也会产生影响(Gersovitz and Hammer,2004)。
从理论上讲,政府可以通过税收与补贴的传统策略把外部性内部化。然而如上文所述,在实践中有大量预防和治疗行为难以观察,不能实施征税或补贴,例如在性传播疾病中过于私密的行为。这种情况提出了次优问题,尤其是当预防或治疗手段出现改进的时候。
流行病学家担心,当预防或治疗手段改进后,人们会放松对传染病的预防和康复的努力程度,他们将该现象称为“抑制解除”(disinhibition)。抑制解除的效应可能非常强大,反而导致感染率上升。不过,流行病学家的关注点不在于此类变化的综合福利影响(包括对预防与治疗的成本的效应),他们也没有区分最优策略得到实施或没有实施的情况,而这从福利角度看非常重要。经济学家担心的则是,当外部性没有得到纠正时,看似不错的创新反而可能导致福利下降,即所谓的贫困化(immiserization)。该原理的一个特定应用场景是:预防和治疗的创新可能导致贫困化,但需要什么条件?
我的一项研究考察了抑制解除和贫困化问题,对基于公式(4)的反复感染模型做了调整,使函数α和β不仅取决于各自的投入,还取决于函数中表示技术进步的一个移位参数(Gersovitz,2010)。在社会计划者把外部性内部化的时候(即采取社会最优策略),预防或治疗的技术改进都不可能导致贫困化。即使感染率上升,在考虑感染的全部影响(包括预防和治疗的成本)后,人们的福利水平依然会得到提高。
该研究显示,如果感染的外部性没有(或不能)通过最优补贴实现内部化,造成贫困化的一个必要条件是:抑制解除的效应非常强大,使感染率在技术进步之后出现提高(Gersovitz,2010)。对于不会使相关健康投入的边际产出a降低的预防技术改进,这种极端的抑制解除效应不可能出现。对这一结论的直观解释是,预防技术的改进会增加人们保持不受感染的概率,从而提高未感染状态的价值。所以在考虑了预防或治疗水平的所有内生调整之后,感染率仍会下降。可是治疗技术的改进却会降低未感染状态的价值,因为在感染后康复、回到未感染状态变得更加容易。即使投入的边际产出b与治疗技术改进彼此独立,在两种对象锁定情形下,治疗的改进仍会导致感染率提高,并可能导致贫困化。这两种情形分别是:(a)预防的对象锁定是未感染者;(b)预防的对象锁定是所有人,且易感染者所占比例超过50%。不过我的研究还提到了特定的函数形式α(a)和β(b),使上述对象锁定情形不会导致感染率提高(Gersovitz,2010)。托克斯瓦尔德(Toxvaerd,2010a,b)的研究同样考察了次优选择问题。拉克达瓦拉等人(Lakdawalla et al.,2006)则针对那些会导致死亡而非康复的疾病,分析了贫困化现象。当然,这一问题并非他们的主要关注点,我们有必要研究能否拓展其分析思路,以找出此类传染病出现贫困化结果的条件。
4.结论
通过政策对传染病做最优应对需要坚实的理论架构,以理解手段和目的,以及在私人部门与公共部门之间应该由谁来做哪些事情。流行病学与经济学的结合可以提供这样的理论基础。经济学进入这一合作领域时间不长,但可以带来重要帮助,而合作的首批成果就是提供深刻的认识。如果没有合适的理论架构,我们将不清楚应该从经验规律中总结些什么,以及如何把这些知识用于评估不同的传染控制策略。
目前,对于建模所需的各组成要件及其对政策定性分析的作用已取得了若干研究进展。不过模型是抽象的理念,针对特定疾病还需要做专门设定。只有结合特定传染病,我们才能枚举预防和治疗的具体方式,并弄清楚付出的努力同取得的成果之间的联系。迄今为止,经济学家针对特定传染病所做的大多数研究都是个人对艾滋病流行的某些行为反应,而且主要面向发达国家的同性恋群体(如Ahituv et al.,1996;Dow and Philipson,1996;Boozer and Philipson,2000;Bhattacharya et al.,2003;Auld,2006;Lakdawalla et al.,2006;Francis,2008)。经济学家还针对其他传染病开展了若干研究,包括恰加斯氏病(CastilloRiqueline et al.,2008)、肠内寄生虫病(Miguel and Kremer,2004)、疟疾(Cohen and Dupas,2010)与血吸虫病(Wiemer,1987)等。这些研究都没有充分采用本文介绍的动态外部性研究方法(Gersovitz and Hammer,2004),因此无法得出与政府干预有关的最终结论。■
(余江 译)
参考文献
Ahituv A, Hotz VJ, Philipson T. 1996. The responsiveness of the demand for condoms to the local prevalence of AIDS.J.Hum.Resour.31:869-97.
Anderson RM, May RM. 1991.Infectious Diseases of Humans: Dynamics and Control.Oxford, UK: Oxford Univ. Press.
Auld MC. 2003. Choices, beliefs, and infectious disease dynamics.J.Health Econ.22:361-77.
Auld MC. 2006. Estimating behavioral response to the AIDS epidemic. Contrib. Econ. Anal. Policy 5:Artic.12.
Barrett S, Hoel M. 2007. Optimal disease eradication. Environ. Dev.Econ.12:627-52.
Bhattacharya J, Goldman D, Sood N. 2003. The link between public and private insurance and HIVrelated mortality. J. Health Econ. 22:1105-22.
Blythe SP, CastilloChavez C, Palmer JS, Cheng M. 1991. Toward a unified theory of sexual mixing and pair formation. Math. Biosci. 107:379-405.
Boozer MA, Philipson TJ. 2000. The impact of public testing for human immunodeficiency virus.
J. Hum. Resour. 35:419-46.
Boulier BL, Datta TS, Goldfarb RS. 2006. Vaccination externalities. B. E. J. Econ. Anal. Policy 7:23.
Brito DI, Sheshinski E, Intriligator MD. 1991. Externalities and compulsory vaccinations. J. Public Econ. 45:69-90.
CastilloRiquelme M, Chalibi Z, Lord J, Guhl F, CampbellLendram D, et al. 2008. Modeling geographic variation in the costeffectiveness of control policies for infectious vector diseases: the example of Chagas disease. J. Health Econ. 27:405-26.
Chen FH. 2004. Rational behavioral response and the transmission of STDs. Theor. Popul. Biol. 66:307-16.
Chen FH. 2006a. A susceptibleinfected epidemic model with voluntary vaccinations. Math. Biol. 53:253-72.
Chen FH. 2006b. On the transmission of HIV with selfprotective behavior and preferred mixing.
Math. Biosci. 199:141-59.
Chen FH. 2009. Modeling the effect of information quality on risk behavior change and the transmission of infectious diseases. Math. Biosci. 217:125-33.
Chen FH, Cottrell A. 2009. Dynamic equilibria in an epidemic model with voluntary vaccinations. J. Biol. Dyn. 3:357-75.
Cohen J, Dupas P. 2010. Free distribution or costsharing? Evidence from a randomized malaria prevention experiment. Q. J. Econ. 125:1-45.
Daley DJ, Gani J. 1999. Epidemic Modelling: An Introduction. Cambridge, UK: Cambridge Univ. Press.
Diekmann O, Heesterbeek JAP. 2000. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. Chichester: Wiley.
Dow WH, Philipson T. 1996. An empirical examination of the implications of assortative matching on the incidence of HIV. J. Health Econ. 15:735-49.
Edlund L, Korn E. 2002. A theory of prostitution. J. Polit. Econ. 110:181-214.
Fine PEM. 1993. Herd immunity: history, theory and practice. Epidemiol. Rev. 15:265-302.
Fine PEM, Clarkson JA. 1986. Individual versus public priorities in the determination of optimal vaccination policies. Am. J. Epidemiol. 124:1012-20.
Francis AM. 2008. The economics of sexuality: the effect of HIV/AIDS on homosexual behavior in the United States. J. Health Econ. 27:675-89.
Francis PJ. 1997. Dynamic epidemiology and the market for vaccinations. J. Public Econ. 63:383-406.
Francis PJ. 2004. Optimal tax/subsidy combinations for the flu season. J. Econ. Dyn. Control 28:2037-54.
Geoffard PY, Philipson T. 1996. Rational epidemics and their public control. Int. Econ. Rev. 37:603-24.
Geoffard PY, Philipson T. 1997. Disease eradication: private versus public vaccination. Am. Econ. Rev. 87:222-30.
Gersovitz M. 2001 (1999). Human behaviour and the transmission of infectious disease: an economists perspective. The Joseph Fisher Lecture. Reprinted in Australias Economy in the International Context: The Joseph Fisher Lectures, Vol. 2, ed. K Anderson, pp. 445-65. Adelaide: Univ. Adelaide.
Gersovitz M. 2003. Births, recoveries, vaccinations and externalities. In Economics for an Imperfect World: Essays in Honor of Joseph E. Stiglitz, ed. R Arnott, B Greenwald, R Kanbur, B Nalebuff, pp. 469-83. Cambridge, MA: Mass. Inst. Technol. Univ. Press.
Gersovitz M. 2010. Disinhibition and immiserization in a model of susceptibleinfectedsusceptible (SIS) diseases. Unpubl. Pap., Johns Hopkins Univ., Baltimore.
Gersovitz M. 2011. HIV testing: principles and practice. World Bank Res. Obs. 26:1-41.
Gersovitz M, Hammer JS. 2003. Infectious diseases, public policy, and the marriage of economics and epidemiology. World Bank Res. Obs.18:129-57.
Gersovitz M, Hammer JS. 2004. The economical control of infectious diseases. Econ. J. 114:1-27.
Gersovitz M, Hammer JS. 2005. Tax/subsidy policies toward vectorborne infectious diseases.J. Public Econ. 89:647-74.
Gertler P, Shah M, Bertozzi SM. 2005. Risky business: the market for unprotected commercial sex. J. Polit. Econ. 113:518-50.
Goldman SM, Lightwood J. 2002. Cost optimization in the SIS model of infectious disease with treatment. Top. Econ. Anal. Policy 2:Artic. 4
Grass D, Caulkins JP, Feichtinger G, Tragler G, Behrens DA. 2008. Optimal Control of Nonlinear Processes: With Applications in Drugs, Corruption, and Terror. Berlin: Springer.
Huang W, Cooke KL, CastilloChavez C. 1992. Stability and bifurcation for a multiplegroup model for the dynamics of HIV/AIDS transmission. SIAM J. Appl. Math. 52:835-54
Keeling MJ, Rohani P. 2008. Modeling Infectious Diseases in Humans and Animals. Princeton: Princeton Univ. Press.
Kremer M. 1996. Integrating behavioral choice into epidemiological models of AIDS. Q. J. Econ. 111:549-73.
KribsZaleta CM, VelascoHerná ndez JX. 2000. A simple vaccination model with multiple endemic states. Math. Biosci.164:183-201.
Kureishi W. 2009. Partial vaccination programs and the eradication of infectious diseases. Econ.Bull.29:2758-69
Lakdawalla D, Sood N, Goldman D. 2006. HIV breakthroughs and risky sexual behavior. Q. J. Econ. 121:1063-102.
Ma Z, Li J, eds. 2009. Dynamical Modeling and Analysis of Epidemics.Hackensack, NJ: World Sci.
Mechoulan S. 2004. HIV testing: a Trojan horse? Top. Econ. Anal. Policy 4:Artic. 18.
Miguel E, Kremer M. 2004. Worms: identifying impacts on education and health in the presence of treatment externalities. Econometrica 72:159-217.
Philipson TJ, Posner RA. 1995. A theoretical and empirical investigation of the effects of public health subsidies for STD testing. Q. J. Econ. 110:445-74.
Philipson TJ. 2000. Economic epidemiology and infectious diseases. In Handbook of Health Economics, ed. AJ Cuyler, JP Newhouse, pp. 1761-69. Amsterdam: North Holland.
Rao V, Gupta I, Lokshin M, Jana S. 2003. Sex workers and the cost of safe sex: the compensating differential for condom use among Calcutta prostitutes. J. Dev. Econ. 71:585-603.
Sethi SP, Staats PW. 1978. Optimal control of some simple deterministic epidemic models. J. Oper. Res. Soc. 29:129-36.
Simon CP, Jacquez JA. 1992. Reproduction numbers and the stability of equilibria of SI models for heterogeneous populations. SIAM J. Appl. Math. 52:541-76.
Ska tun JD. 2003. The overprovision of infectious disease medicine. Econ. Lett. 80:61-66.
Skiba AK. 1978. Optimal growth with a convexconcave production function. Econometrica 46:527-39.
Toxvaerd F. 2010a. Infection, acquired immunity and externalities in treatment. Unpubl. Pap., Cambridge Univ., Cambridge, UK.
Toxvaerd F. 2010b. Recurrent infection and externalities in prevention. Unpubl. Pap., Cambridge Univ., Cambridge, UK.
Whitaker L, Rentin AM. 1992. A theoretical problem of interpreting the recently reported increase of homosexual gonorrhea. Eur. J. Epidemiol. 8:187-91.
Wickwire K. 1977. Mathematical models for the control of pests and infectious diseases: a survey. Theor. Popul. Biol. 11:182-238.
Wiemer C. 1987. Optimal disease control through combined use of preventive and curative measures. J. Dev. Econ. 25:301-19.
Xu X. 1999. Technological improvements in vaccine efficacy and individual incentive to vaccinate. Econ. Lett. 65:359-64.